Một nguời đi xe máy từ Hà Nam về Phủ Lý với quãng đường 45km. Trong nửa thời gian đầu đi với vận tốc v 1 , nửa thời gian sau đi với v 2 = 2 3 v 1 . Xác định v 1 , v 2 biết sau 1h30 phút nguời đó đến B.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 8 2021
a,\(=>vtb1=\dfrac{S}{\dfrac{\dfrac{1}{2}S}{v1}+\dfrac{\dfrac{1}{2}S}{v2}}=\dfrac{S}{\dfrac{S}{2v1}+\dfrac{S}{2v2}}=\dfrac{S}{\dfrac{S\left(v1+v2\right)}{2v1v2}}=\dfrac{2v1v2}{v1+v2}\left(km/h\right)\)\(=>vtb2.t=\dfrac{1}{2}t.v1+\dfrac{1}{2}t.v2\)
\(=>vtb2.t=\dfrac{1}{2}t\left(v1+v2\right)=>vtb2=\dfrac{1}{2}\left(v1+v2\right)\left(km/h\right)\)
b,\(vtb1-vtb2=\dfrac{2v1v2}{v1+v2}-\dfrac{v1+v2}{2}=\dfrac{4v1v2-\left(v1+v2\right)^2}{2\left(v1+v2\right)}\)
\(=\dfrac{4v1v2-v1^2-2v1v2-v2^2}{2\left(v1+v2\right)}=\dfrac{-\left(v1-v2\right)^2}{2\left(v1+v2\right)}\le0\)
\(=>vtb1\le vtb2\)=> xe thứ 2 đến B trước
và đến trước trong
\(t=\dfrac{L}{vtb1}-\dfrac{L}{vtb2}=\dfrac{L\left(vtb2-vtb1\right)}{vtb2.vtb1}\left(h\right)\)
27 tháng 6 2021
a, theo bài ra
nửa quãng đường đầu xe thứ nhất đi trong \(t1=\dfrac{\dfrac{1}{2}S}{v1}=\dfrac{\dfrac{1}{2}S}{40}=\dfrac{S}{80}h\)
nửa quãng đường sau xe thứ nhất đi trong \(t2=\dfrac{\dfrac{1}{2}S}{v2}=\dfrac{\dfrac{1}{2}S}{60}=\dfrac{S}{120}\left(h\right)\)
\(=>Vtb1=\dfrac{S}{t1+t2}=\dfrac{S}{\dfrac{S}{80}+\dfrac{S}{120}}=\dfrac{S}{\dfrac{200S}{9600}}=\dfrac{9600}{200}=48km/h\)
* đối với xe 2
quãng đường xe 2 đi trong nửa tgian đầu:\(S1=\dfrac{1}{2}t.40=20t\left(km\right)\)
quãng đường xe 2 đi trong nửa tgian sau: \(S2=\dfrac{1}{2}t.60=30t\left(km\right)\)
\(=>S=vtb2.t\)\(=30t+20t=50t\)
\(=>vtb2=50km/h\)
27 tháng 6 2021
b, do \(vtb1< vtb2\left(48< 50\right)\) do đó xe thứ 2 về B trước xe thứ nhất
đổi \(20s=\dfrac{1}{180}h\)
theo bài ra xe thứ nhất về đích sau xe thứ 2 là 20s\(=\dfrac{1}{180}h\)
\(=>t3-t4=\dfrac{1}{180}\)
\(< =>\dfrac{S}{vtb1}-\dfrac{S}{vtb2}=\dfrac{1}{180}< =>\dfrac{S}{48}-\dfrac{S}{50}=\dfrac{1}{180}\)
\(< =>\dfrac{2S}{2400}=\dfrac{1}{180}=>360S=2400=>S=\dfrac{2400}{360}=\dfrac{20}{3}km\)
2 tháng 8 2016
\(S_1+S_2=45\) (km)
\(\Leftrightarrow v_1\frac{1,5}{2}+\frac{2}{3}v_1\frac{1,5}{2}=45\Rightarrow v_1=10,4\left(\frac{km}{gi\text{ờ}}\right)\Rightarrow v_2=6,9\left(\frac{km}{gi\text{ờ}}\right)\)
LA
22 tháng 6 2017
Tính vận tốc trung bình của xe đi từ A đến B
vtb = s/t
theo bài ra ta có : s/2 = 20*t1 và s/2 = 60*t2
=> vtb = s/( t1 + t2) = s/ ( s/40 + s/ 120 ) = 30 (km/h)
Tính vận tốc trung bình của xe đi từ B đến A
theo bài ra ta cũng có
t/2 = s1/20 và t/2 = s2/60
=> vtb" = (s1 + s2 )/t = ( 10t + 30t )/t = 40 ( km/h)
Mà nếu xe từ B xuất phát muộn hơn so với xe xuất phát từ A 30phút = 1/2 h thì 2 xe đến địa điểm cùng 1 lúc
=> sA-B = 30*t
sB-A = 40 * ( t - 1/2)
Mà sA-B = sB-A => 30*t = 40 * ( t - 1/2) => t= 2 (h)
Vậy s = 60 ( km)
Chọn chiều dương từ A đến B
Gốc thời gian lúc bắt đầu xuất phát
Gốc tọa độ tại A
Viết phương trình chuyển động của xe A : xA = 30*t
Của xe B là xB = 60 - 40*t
Để hai xe gặp nhau thì xA = xB
=> 30*t = 60 - 40*t => t = 6/7 ( h)
Vậy hai xe xuất phát cùng lúc thì chúng sẽ gặp nhau cách A 1 khoảng xA = xB = 180/7 ( km )
27 tháng 8 2020
Gọi độ dài quãng đường AB là s (km)
- Tính vận tốc trung bình của xe đi từ A đến B
vtb = s/t
theo bài ra ta có : s/2 = 20*t1 và s/2 = 60*t2
=> vtb = s/( t1 + t2) = s/ ( s/40 + s/ 120 ) = 30 (km/h)
- Tính vận tốc trung bình của xe đi từ B đến A
theo bài ra ta cũng có
t/2 = s1/20 và t/2 = s2/60
=> vtb" = (s1 + s2 )/t = ( 10t + 30t )/t = 40 ( km/h)
Mà nếu xe từ B xuất phát muộn hơn so với xe xuất phát từ A 30phút = 1/2 h thì 2 xe đến địa điểm cùng 1 lúc
=> sA-B = 30*t
sB-A = 40 * ( t - 1/2)
Mà sA-B = sB-A => 30*t = 40 * ( t - 1/2) => t= 2 (h)
Vậy s = 60 ( km)
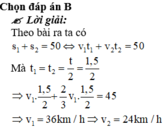
Giải: Theo bài ra ta có
s 1 + s 2 = 50 ⇔ v 1 t 1 + v 2 t 2 = 50
Mà t 1 = t 2 = t 2 = 1 , 5 2
⇒ v 1 . 1 , 5 2 + 2 3 v 1 . 1 , 5 2 = 45 ⇒ v 1 = 36 k m / h ⇒ v 2 = 24 k m / h