Một vật dao động điều hoà khi đi qua vị trí cân bằng theo chiều dương ở thời điểm ban đầu. Khi vật có li độ 3cm thì vận tốc của vật bằng 8π cm/s và khi vật có li độ bằng 4cm thì vận tốc của vật bằng 6π cm/s. Phương trình dao động của vật có dạng:
A. x = 5cos(2πt-π/2)(cm).
B. x = 5cos(2πt + π/2)(cm).
C.x = 10cos(2πt-π/2)(cm).
D. x = 5cos(2πt + π) (cm).


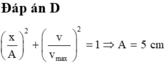
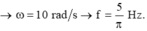
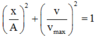
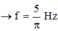



Chọn A
+ Thay (x1 = 3cm; v1 = 8π cm/s) và (x2 = 4cm; v2 = 6π cm/s) vào ta được hệ phương trình hai ẩn A2 và
ta được hệ phương trình hai ẩn A2 và 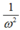
. Giải hệ phương trình ta được A = 5cm và ω = 2π rad/s.
+ Tìm giá trị các đại lượng thay vào:
+ t = 0: vật qua vị trí cân bằng theo chiều dương => φ = - π/2 rad.
+ Thay số: x = 5cos(2πt - π/2)(cm).