Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
Khi đó
- Số cách chọn chữ số α có 5 cách chọn vì α ≠ 0 .
- Số cách chọn chữ số b có 5 cách chọn vì b ≠ α .
- Số cách chọn chữ số c có cách chọn vì c ≠ α và c ≠ b .
Do đó tập S có 5.5.4 = 100 phần tử.
Không gian mẫu là chọn ngẫu nhiên1 số từ tập S .
Suy ra số phần tử của không gian mẫu là Ω = C 100 1 = 100 .
Gọi X là biến cố "Số được chọn có chữ số cuối gấp đôi chữ số đầu". Khi đó ta có các bộ số là 1 b 2 hoặc 2 b 4 thỏa mãn biến cố X và cứ mỗi bộ thì b có 4 cách chọn nên có tất cả số thỏa yêu cầu.
Suy ra số phần tử của biến cố X là Ω X = 8 .
Vậy xác suất cần tính P ( X ) = Ω X Ω = 8 100 = 2 25 .
Giả sử a là chữ số hàng chục và b là chữ số hàng đơn vị của số cần tìm
Ta có:
Tập hợp A:
Số cần tìm là số có hai chữ số nên chữ số hàng chục a ≠ 0.
Vì a + b = 8 nên a chỉ có thể lấy các giá trị 1, 2, 3, 4, 5, 6, 7, 8.
Vậy, Tập hợp A = {17 ; 26 ; 35 ; 44 ; 53 ; 62 ; 71 ; 80}.
Tập hợp B:
Số cần tìm là số có hai chữ số nên chữ số hàng chục a ≠ 0.
Số cần tìm được tạo thành từ hai trong bốn số 0 ; 3 ; 5 ; 8
Vậy, Tập hợp B = {30 ; 35 ; 38 ; 50 ; 53 ; 58 ; 80 ; 83 ; 85}.
có 1 phần tử
A={7}có 1 phần tử
B là tập hợp rỗng
D là tập hợp rỗng
có 1 phần tử
tập hợp A có 4 tập hợp con
ong số học, bội số chung nhỏ nhất (hay còn gọi tắt là bội chung nhỏ nhất, viết tắt là BCNN, tiếng Anh: least common multiple hoặc lowest common multiple (LCM) hoặc smallest common multiple) của hai số nguyên a và b là số nguyên dương nhỏ nhất chia hết cho cả a và b.[1] Tức là nó có thể chia cho a và b mà không để lại số dư. Nếu a hoặc b là 0, thì không tồn tại số nguyên dương chia hết cho a và b, khi đó quy ước rằng LCM(a, b) là 0.
Định nghĩa trên đôi khi được tổng quát hoá cho hơn hai số nguyên dương: Bội chung nhỏ nhất của a1,..., an là số nguyên dương nhỏ nhất là bội số của a1,..., an.
Gọi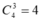
là số cần lập .
Vì x là số chẵn nên e ∈ {0; ;2; 4; 6}. Ta xét các trường hợp sau
e = 0 ⇒ e có 1 cách chọn
Số cách chọn
là một chỉnh hợp của 6 phần tử
Số cách chọn các chữ số còn lại là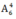
Do đó trường hợp này có tất cả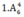
số
e ≠ 0 ⇒ e có 3 cách chọn
Với mỗi cách chọn e ta có a ∈ A \ {0;e} nên có 5 cách chọn a.
Số cách chọn các số còn lại là: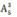
Do đó trường hợp này có tất cả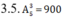
số
Vậy có tất cả: 360 + 900 = 1260 số thỏa yêu cầu bài toán.
Chọn A.