Cho hàm số y = f(x) có lim x → + ∞ f ( x ) = 3 và lim x → - ∞ f ( x ) = - 3 Khẳng định nào sau đây là khẳng định đúng?
A. Đồ thị hàm số đã cho có đúng một tiệm cận ngang
B. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng x = 3 và x = -3
C. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng y = 3 và y = -3
D. Đồ thị hàm số đã cho không có tiệm cận ngang


Đáp án C.
Ta có: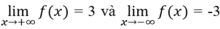
=> y = 3, y = -3 là hai tiệm cận ngang.