Tìm tập hợp tất cả các giá trị của tham số thực m để hàm số y = ln x 2 + 1 - m x + 1 đồng biến trên khoảng ( -∞; +∞).
A. ( - ∞ ; - 1 ]
B. ( - ∞ ; - 1 )
C. - 1 ; 1
D. Đáp án khác
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: y ' = 2 x x 2 + 1 = - m .
Hàm số Y= ln( x2+ 1) –mx+1 đồng biến trên R khi và chỉ khi y’≥ 0 với mọi x.
⇔ g ( x ) = 2 x x 2 + 1 ≥ m , ∀ x ∈ - ∞ ; + ∞ . g ' ( x ) = - 2 x 2 + 2 ( x 2 + 1 ) 2 = 0 ⇔ x = ± 1 .
Bảng biến thiên:
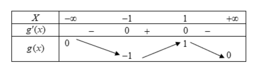
Dựa vào bảng biến thiên ta có: g ( x ) = 2 x x 2 + 1 ≥ m với mọi x khivà chỉ khi m≤ -1.
Chọn C.

Chọn đáp án C
Phương pháp
Hàm số y=f(x) có TXĐ D=R đồng biến trên nếu:

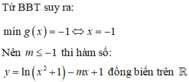

1.
\(y'=m-3cos3x\)
Hàm đồng biến trên R khi và chỉ khi \(m-3cos3x\ge0\) ; \(\forall x\)
\(\Leftrightarrow m\ge3cos3x\) ; \(\forall x\)
\(\Leftrightarrow m\ge\max\limits_{x\in R}\left(3cos3x\right)\)
\(\Leftrightarrow m\ge3\)
2.
\(y'=1-m.sinx\)
Hàm đồng biến trên R khi và chỉ khi:
\(1-m.sinx\ge0\) ; \(\forall x\)
\(\Leftrightarrow1\ge m.sinx\) ; \(\forall x\)
- Với \(m=0\) thỏa mãn
- Với \(m< 0\Rightarrow\dfrac{1}{m}\le sinx\Leftrightarrow\dfrac{1}{m}\le\min\limits_R\left(sinx\right)=-1\)
\(\Rightarrow m\ge-1\)
- Với \(m>0\Rightarrow\dfrac{1}{m}\ge sinx\Leftrightarrow\dfrac{1}{m}\ge\max\limits_R\left(sinx\right)=1\)
\(\Rightarrow m\le1\)
Kết hợp lại ta được: \(-1\le m\le1\)

Đáp án D
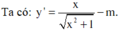
Để hàm số đã cho đồng biến trên khoảng − ∞ ; + ∞ thì y ' > 0 , ∀ x ∈ ℝ
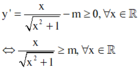
Xét hàm số y = x x 2 + 1 có y ' = 1 x 2 + 1 x 2 + 1 > 0 , ∀ x ∈ ℝ => Hàm số y' luôn đồng biến.
Ta có: lim x → − ∞ x x 2 + 1 = − 1
Vậy để hàm số đã cho đồng biến trên khoảng − ∞ ; + ∞ thì m ≤ − 1 .

Đáp án D
y ' = 2 x x 2 + 1 − m = 2 x − m x 2 + 1 x 2 + 1 T H 1 : m = 0 ⇔ 2 x x 2 + 1 > 0 ⇔ x > 0 T H 2 : m ≠ 0
Hàm số đồng biến trên khoảng
− ∞ ; + ∞ ⇔ − m x 2 + 2 x − m > 0 ∀ x ∈ ℝ
⇔ − m > 0 Δ ' = 1 − m 2 ≤ 0 ⇔ m < 0 m ≥ 1 m ≤ − 1 ⇔ m ≤ − 1
Chọn A.
Ta có: y ' = 2 x x 2 + 1 - m
Hàm số y = ln x 2 + 1 - m x + 1 đồng biến trên khoảng( -∞; +∞). Khi và chỉ khi y’ ≥0 với mọi . ⇔ g ( x ) = 2 x x 2 + 1 ≥ m , ∀ x ∈ - ∞ ; + ∞
Ta có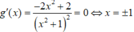
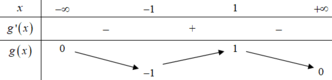
Bảng biến thiên:
Dựa vào bảng biến thiên ta có: