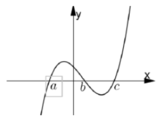
Cho hàm số y= f( x) =ax4+ bx3+ cx2+ dx+ e và hàm số y= f’( x) có đồ thị như hình vẽ bên. Biết f( b) < 0 , hỏi đồ thị hàm số y= f(x) cắt trục hoành tại nhiều nhất bao nhiêu điểm?
A. 1
B. 2
C. 3
D. 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có
![]()
Đồ thị hàm số ![]() cắt trục hoành tại bốn điểm phân biệt bên phương trình
cắt trục hoành tại bốn điểm phân biệt bên phương trình ![]() , với
, với ![]() là các nghiệm.
là các nghiệm.
Suy ra
![]()
![]()
![]()
![]()
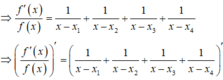
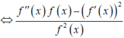
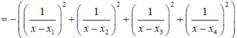
Nếu ![]() với
với ![]() thì
thì ![]() ,
, ![]()
![]() .
.
Nếu ![]() thì
thì 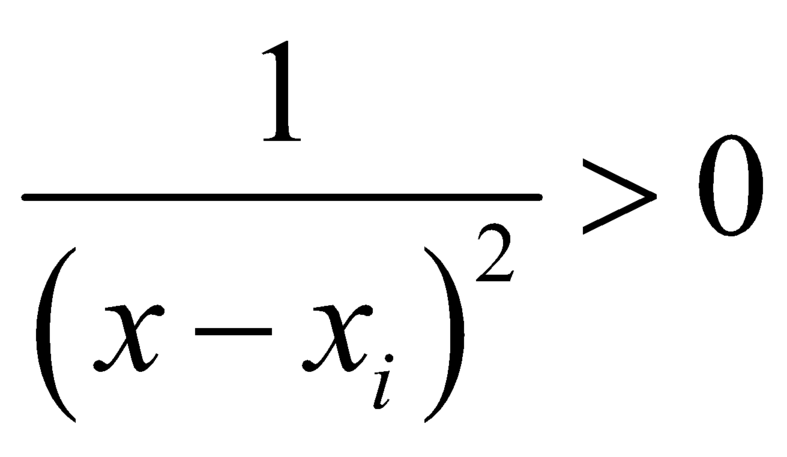 ,
, ![]() .
.
Suy ra ![]()
![]() .
.
Vậy phương trình ![]() vô nghiệm hay phương trình
vô nghiệm hay phương trình ![]() vô nghiệm.
vô nghiệm.
Do đó, số giao điểm của đồ thị hàm số và trục hoành là 0
Đáp án A

Đáp án B.
Từ đồ thị hàm số y = f ' ( x ) ta có bảng biến thiên:

Từ bảng biến thiên ta có f ( b ) > f ( a ) > 0
Quan sát đồ thị y = f ' ( x ) , dùng phương pháp tích phân để tính diện tích.
Ta có ∫ a b f ' ( x ) d x < ∫ a c 0 - f ' ( x ) d x ⇒ f ( c ) < f a
Nếu f c < 0 thì đồ thị hàm số y = f ( x ) cắt trục hoành tại 2 điểm phân biệt.
Nếu f c = 0 thì đồ thị hàm số y = f ( x ) tiếp xúc với trục hoành tại 1 điểm.
Nếu f c > 0 thì đồ thị hàm số y = f ( x ) không cắt trục hoành.
Vậy đồ thị hàm số y = f ( x ) cắt trục hoành tại nhiều nhất 2 điểm.

Chọn C
Trên đoạn [ - 1; 1] đồ thị hàm số y= f’( x) nằm phía trên trục hoành.
=> Trên đoạn [ - 1; 1] thì f’( x) > 0.
=> Trên đoạn [ - 1; 1] thì hàm số y= f( x) đồng biến

Đáp án B
Giả thiết
![]()
Đặt
![]()
thì
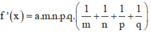
Và
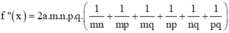
Khi đó, phương trình
![]() (vô nghiệm)
(vô nghiệm)
Vậy đồ thị hàm số y = g(x) không cắt trục hoành.
Ta có bảng biến thiên như hình vẽ bên.
Vì f( b) < 0 nên rõ ràng có nhiều nhất 2 giao điểm.
Chọn B.