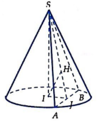
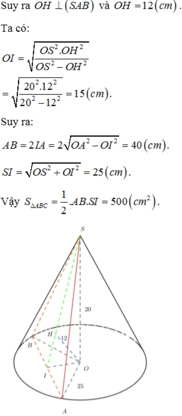
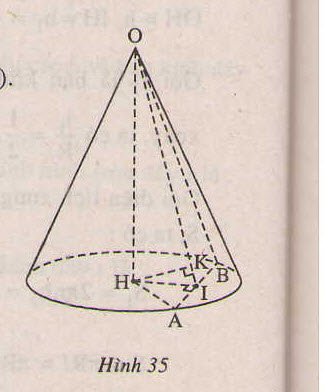
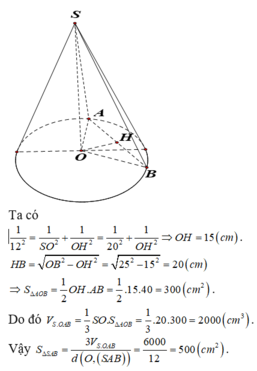
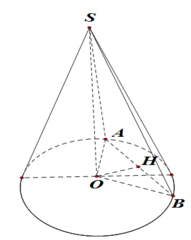
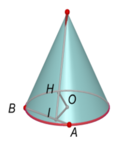
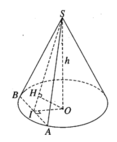
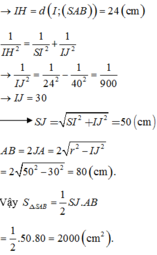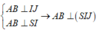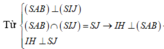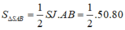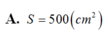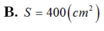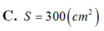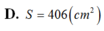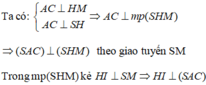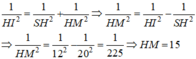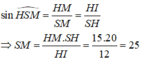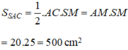Cho hình nón tròn xoay có đường cao h=40 (cm), bán kính đáy r=50 (cm). Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện là 24 (cm). Tính diện tích của thiết diện
A. S = 800 cm 2
B. S = 1200 cm 2
C. S = 1600 cm 2
D. S = 2000 cm 2