Chứng minh rằng A = 2 2 + 2 3 + 2 6 chia hết cho 11
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
7 tháng 9 2018
Đúng(0)
Những câu hỏi liên quan
PB
0
23 tháng 10 2015
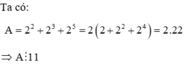
TA CÓ:
A=30+3+32+33+........+311
(30+3+32+33)+....+(38+39+310+311)
3(0+1+3+32)+......+38(0+1+3+32)
3.13+....+38.13 cHIA HẾT CHO 13 NÊN A CHIA HẾT CHO 13( đpcm)
25 tháng 3 2020
a) Ta có: \(\overline{abcdeg}=\overline{ab}.1000+\overline{cd}.100+\overline{eg}\)
\(=\overline{ab}.999+\overline{cd}.99+\overline{ab}+\overline{cd}+\overline{eg}\)
\(=\left(\overline{ab}.999+\overline{cd}.99\right)+\left(\overline{ab}+\overline{cd}+\overline{eg}\right)\)
Vì \(\left(\overline{ab}.999+\overline{cd}.99\right)⋮11\)
và \(\left(\overline{ab}+\overline{cd}+\overline{cd}\right)⋮11\left(gt\right)\)
\(\Rightarrow\overline{abcdeg}⋮11\left(đpcm\right)\)
b) \(\cdot A=2+2^2+2^3+...+2^{60}\)
\(A=\left(2+2^2\right)+...+\left(2^{50}+2^{60}\right)\)
\(A=2.3+...+2^{50}.3\)
\(A=3\left(2+..+2^{50}\right)⋮3\)
các trường hợp còn lại tự lm nhé!!
XO
2 tháng 7 2019
1) Ta có : 11a + 22b + 33c
= 11a + 11.2b + 11.3c
= 11.(a + 2b + 3c) \(⋮\)11
=> 11a + 22b + 33c \(⋮\)11
2) 2 + 22 + 23 + ... + 2100
= (2 + 22) + (23 + 24) + ... + (299 + 2100)
= (2 + 22) + 22.(2 + 22) + ... + 298.(2 + 22)
= 6 + 22.6 + ... + 298.6
= 6.(1 + 22 + .. + 298)
= 2.3.(1 + 22 + ... + 298) \(⋮\)3
=> 2 + 22 + 23 + ... + 2100 \(⋮\)3
3) Ta có: abcabc = abc000 + abc
= abc x 1000 + abc
= abc x (1000 + 1)
= abc x 1001
= abc .7. 13.11 (1)
= abc . 7 . 13 . 11 \(⋮\)7
=> abcabc \(⋮\)7
=> Từ (1) ta có : abcabc = abc x 7.11.13 \(⋮\)11
=> abcabc \(⋮\)11
=> Từ (1) ta có : abcabc = abc . 7.11.13 \(⋮\) 13
=> => abcabc \(⋮\)13
2 tháng 7 2019
1
.\(11a+22b+33c=11\left(a+2b+3c\right)⋮11\)
\(\Rightarrow11a+22b+33c⋮11\left(đpcm\right)\)
hc tốt
KC
12 tháng 11 2015
Ban "ten to sieu dai yyyyyyyyyyyyyyyyyyyyyyy...." oi! ban dung khoe ten nua. ten dai koa dk j dau ma khoe.
LT
2
16 tháng 11 2018
1:\(A=1+3+3^2+3^3+...+3^{11}\)
\(A=\left(1+3\right)+\left(3^2+3^3\right)+...+\left(3^{10}+3^{11}\right)\)
\(A=4+3^2\cdot\left(1+3\right)+...+3^{10}\cdot\left(1+3\right)\)
\(A=4+3^2\cdot4+....+3^{10}\cdot4\)
\(A=4\cdot\left(1+3^2+...+3^{10}\right)\) chia hết cho 4
Vì ta có 4 chia hết cho 4 => A có chia hết cho 4
Vậy A chia hết cho 4
16 tháng 11 2018
2:
\(C=5+5^2+5^3+...+5^8\) chia hết cho 30
\(C=\left(5+5^2\right)+...+\left(5^7+5^8\right)\)
\(C=30+5^2\cdot\left(5+5^2\right)+...+5^6\cdot\left(5+5^2\right)\)
\(C=30\cdot1+5^2\cdot30+...5^6\cdot30\)
\(C=30\cdot\left(5^2+...+5^6\right)\)
Vì ta có 30 chia hết cho 30 nên suy ra C có chia hết cho 30
Vậy C có chia hết cho 30
18 tháng 10 2015
(1+23)+(2+24)+...+(28+211)
9+2(1+23)+...+28(1+23)
9(1+2+...+28) chia hết cho 9
=>( 2^0+2^1+2^2 + ...+2^11) chia hết cho 9
18 tháng 10 2015
c)(5+52)+(53+54)+...+(599+5100)
5(1+5)+53(1+5)+...+599(1+5)
6(5+53+...+599) chia hết cho 3
