Xét các số nguyên dương chia hết cho 3. Tổng số 50 số nguyên dương đầu tiên của dãy số đó bằng
A. 3675
B. 3750
C. 3825
D. 3900
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 7 2022
#include <bits/stdc++.h>
#define ll long long
using namespace std;
ll i, j, n, a[1000005], dem = 0, m;
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n;
for (i = 1; i <= n; i++)
{
cin >> a[i];
if (a[i] % 3 == 0)
{
n--;
i--;
}
}
for (i = 1; i <= n; i++)
{
cout << a[i] << " ";
}
cout<<endl;
for(i=1;i<=n;i++)
{
if(a[i]%5==0)
{
for(j=i;j<=n;j++)
{
a[j]=a[j+1];
}
n--;
i--;
}
}
for(i=1;i<=n;i++)
{
cout<<a[i]<<" ";
}
return 0;
}
2 tháng 11 2021
a: #include <bits/stdc++.h>
using namespace std;
long long n,i,x,dem;
int main()
{
cin>>n;
dem=0;
for (i=1; i<=n; i++)
{
cin>>x;
if (x%2!=0) dem++;
}
cout<<dem;
return 0;
}
11 tháng 10 2021
a, Tham Khảo: tìm số nguyên tố p biết p+1 là tổng của n số nguyên dương đầu tiên, trong đó n là một số tự nhiên nào đó câu hỏi 1272037 - hoidap247.com
\(b,B=\left(1+2^2+2^4\right)+\left(2^6+2^8+2^{10}\right)+...+\left(2^{1996}+2^{1998}+2^{2000}\right)\\ B=\left(1+2^2+2^4\right)+2^6\left(1+2^2+2^4\right)+...+2^{1996}\left(1+2^2+2^4\right)\\ B=\left(1+2^2+2^4\right)\left(1+2^6+...+2^{1996}\right)\\ B=21\left(1+2^6+...+2^{1996}\right)⋮21\)
NL
30 tháng 10 2021
a) nếu P = 2 thì P + 1 = 2 + 1 = 3 = 1 + 2 (chọn)
nếu P = 3 thì P + 1 = 3 + 1 = 4 = 1 + 2 + 1 (loại)
xét : ta có thể phân các tổng lớn hơn 3 thành tổng của 3 số hạng khác nhau nhưng số 4 thì không thể phân thành 3 số nguyên dương khác nhau
vì số 3 cũng không thể nên nhưng khác với số 4 là nó chỉ có thể phân thành tổng của 2 hay 1 số nguyên dương khác nhau
=>n = 2 và P = 2
cái này là mk tự nghĩ ra thôi nha , có gì sai mong mng chỉ bảo
Số các số nguyên dương thỏa mãn bài toán lập thành một cấp số cộng với số hạng đầu u 1 = 3 và công sai d = 3
Do đó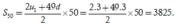
Chọn C.