Tìm tất cả các giá trị thực của m để phương trình x 2 − 4 x + 6 + 3 m = 0 có nghiệm thuộc đoạn − 1 ; 3 :
A. 2 3 ≤ m ≤ 11 3
B. − 11 3 ≤ m ≤ − 2 3
C. − 1 ≤ m ≤ − 2 3
D. − 11 3 ≤ m ≤ − 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(x-4\sqrt{x+3}+m=0\)
\(\Leftrightarrow x+3-4\sqrt{x+3}-3+m=0\left(1\right)\)
\(đăt:\sqrt{x+3}=t\left(t\ge0\right)\)
\(\left(1\right)\Leftrightarrow t^2-4t-3+m=0\Leftrightarrow f\left(t\right)=t^2-4t-3=-m\left(2\right)\)
\(\left(1\right)-có-2ngo-phân-biệt\Leftrightarrow\left(2\right)có-2ngo-phân-biệt-thỏa:t\ge0\)
\(\Rightarrow f\left(0\right)=-3\)
\(\Rightarrow f\left(t\right)min=\dfrac{-\Delta}{4a}=-7\Leftrightarrow t=2\)
\(\Rightarrow-7< -m\le-3\Leftrightarrow3\le m< 7\)
\(t^2-4t-3+m=0\Leftrightarrow t^2-4t-3=-m\)
\(có-2nghiệm-pb-trên[0;\text{+∞})\)
\(xét-bảng-biến-thiên-củaf\left(t\right)=t^2-4t-3,trên[0;\text{+∞})\)
dựa vào bảng biến thiên ta thấy số nghiệm của phương trình f(t)
là số giao điểm của đường thẳng y=-m
\(\Rightarrow-7< -m\le-3\Leftrightarrow3\le m< 7\)

Đáp án A
Điều kiện: x > 0 .
4 log 4 2 x − 2 log 2 x + 3 − m = 0 ⇔ 4. 1 4 . log 2 2 x − 2 log 2 x + 3 − m = 0 ⇔ log 2 2 x − 2 log 2 x + 3 − m = 0 1 .
Đặt t = log 2 x ta có (1) tương đương
t 2 − 2 t + 3 − m = 0 ⇔ t 2 − 2 t + 3 = m .
Ta tìm giá trị của m để t 2 − 2 t + 3 − m = 0 có nghiệm thuộc đoạn 1 ; 2 .
Khảo sát hàm y t = t 2 − 2 t + 3.
Ta có y ' t = 2 t − 2 = 0 ⇔ t = 1.
Bảng biến thiên
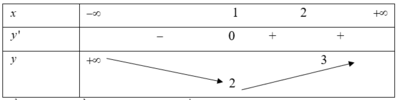
Để thỏa mãn đề bài thì 2 ≤ m ≤ 3 .

Đáp án D
Điều kiện: x > 0.
Đặt t = log 2 x . Khi đó
4 log 2 4 x − 2 log 2 x + 3 − m = 0 ⇔ 4. 1 4 log 2 2 x − 2 log 2 x + 3 − m = 0 ⇔ t 2 − 2 t + 3 − m = 0.
Để thỏa mãn đề bài thì phương trình t 2 − 2 t + 3 − m = 0 có nghiệm thuộc đoạn − 1 ; 2
t 2 − 2 t + 3 − m = 0 ⇔ t 2 − 2 t + 3 = m .
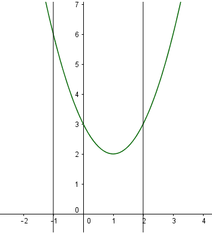
Từ đồ thị hàm số y = t 2 − 2 t + 3 nhân thấy 2 ≤ m ≤ 6 thỏa mãn điều kiện đề bài.
Ta có: x 2 - 4 x + 6 + 3 m = 0 ⇔ 3 m = - x 2 + 4 x - 6
Số nghiệm của phương trình x 2 - 4 x + 6 + 3 m = 0 là số giao điểm của đường thẳng y = 3 m và parabol y = - x 2 + 4 x - 6
Parabol y = - x 2 + 4 x - 6 có hoành độ đỉnh x = 2 ∈ - 1 ; 3 , hệ số a = - 1 < 0 nên đồng biến khi x < 2 và nghịch biến khi x > 2 .
Bảng biến thiên của hàm số y = - x 2 + 4 x - 6 trên đoạn - 1 ; 3 :
Từ bảng biến thiên ta thấy, nếu phương trình có nghiệm trên đoạn - 1 ; 3 thì đường thẳng y = 3 m phải cắt parabol tại ít nhất 1 điểm có hoành độ thuộc đoạn - 1 ; 3 .
Phương trình có nghiệm thuộc đoạn - 1 ; 3 ⇔ - 11 ≤ 3 m ≤ - 2 ⇔ − 11 3 ≤ m ≤ − 2 3
Đáp án cần chọn là: B