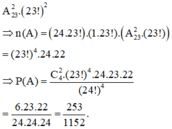Có 3 bạn A, B, C cùng giải 1 bài thi môn XSTK. Xác suất để mỗi bạn giải được bài lần lượt là 1/8

Ba bạn Vui, Học, Toán cùng thi giải toán. Trong cùng một thời gian, Vui giải được 12 bài, Học giải được ít hơn trung bình của 3 bạn là 1 bài; Toán giải được nhiều hơn trung bình của 3 bạn là 5 bài. Hỏi: a. Trung bình mỗi bạn giải được bao nhiêu bài toán? b. Học và Toán đã giải được bao nhiêu bài toán?

#Toán lớp 4

4

NM

Nguyễn Minh Quang

Giáo viên

25 tháng 2 2021

ta có : tổng số bài của Học và toán nhiều hơn trung bình ba bạn là 4 bài

Do đó trung bình của ba bạn là \(12+4=16\) bài

Học đã gải được \(16-1=15\) bài

Toán đã giải được \(16+5=21\)bà

Đúng(0)

BM

Bùi Minh Đức 2

22 tháng 12 2021

bằng 5

Đúng(0)

LM

Lý Mai Trang

1 tháng 12 2019 - olm

Bài 1: Số học sinh lớp 7B thích thể thao, âm nhạc, mĩ thuật lần lượt tỉ lệ với 2,3,5. Biết số học sinh mĩ thuật nhiều hơn thích âm nhạc là 6 học sinh. Tính số học sinh mỗi loại

Bài 2: Ba bạn A,B,C giải đc 172 bài toán trong cùng một thời gian. Để giải xong 1 bài A,B,C cần 5,6,9 phút. Tính xem mỗi bạn giải được bao nhiêu bài?

CÁC BẠN GIÚP MK VS MK ĐAG CẦN GẤP

THANKS!

#Toán lớp 7

1

TG

Trần Gia Linh

1 tháng 12 2019

Bài 1:

Gọi số học sinh lớp 7B thích thể thao, âm nhạc, mĩ thuật thứ tự là: x, y, z

Vì số học sinh lớp 7B thích thể thao, âm nhạc, mĩ thuật lần lượt tỉ lệ với 2,3,5 nên ta có: \(\frac{x}{2}=\frac{y}{3}=\frac{z}{5}\)

Vì số học sinh mĩ thuật nhiều hơn số học sinh âm nhạc là 6 học sinh nên: z-y=6

Áp dụng tính chất của dãy tỉ số bằng nhau suy ra:

\(\frac{x}{2}=\frac{y}{3}=\frac{z}{5}=\frac{z-y}{5-3}=\frac{6}{2}=3\)

=> x = 3x2= 6

y= 3x3=9

z= 3x5=15

Vậy số học sinh lớp 7B thích thể thao là: 6 hs

số học sinh lớp 7B thích âm nhạc là: 9 hs

số học sinh lớp 7b thích mĩ thuật là: 15 hs

Đúng(0)

KD

kẻ dấu mặt

8 tháng 4 2016 - olm

Trong năm học vừa qua trường Thành Công A có 30 bạn thi học sinh giỏi hai môn Toán và Tiếng Việt. Trong số đó có 17 bạn thi môn Toán và 18 bạn thi môn Tiếng Việt. Hỏi Trường có bao nhiêu bạn thi cả hai môn?Lớp 5A có 35 học sinh làm bài kiểm tra Toán. Đề bài gồm có 3 bài toán. Sau khi kiểm tra, cô giáo tổng hợp được kết quả như sau: Có 20 em giải được bài toán thứ nhất, 14 em giải được...

Đọc tiếp

#Toán lớp 4

0

PT

Pham Trong Bach

30 tháng 7 2018

Trong kì thi THPT Quốc Gia, mỗi phòng thi gồm 24 thí sinh được sắp xếp vào 24 bàn khác nhau. Bạn Nam là một thí sinh dự thi, bạn đăng kí 4 môn thi và cả 4 lần đều thi tại 1 phòng duy nhất. Giả sử giám thị xếp thí sinh vào vị trí một cách ngẫu nhiên, tính xác suất để trong 4 lần thi thì bạn Nam có đúng 2 lần ngồi vào cùng 1 vị trí. A. 26 35 B. 899 1152 C. 253 ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

30 tháng 7 2018

Chọn C.

Phương pháp:

Gọi A : “bạn Nam có đúng 2 lần ngồi vào cùng 1 vị trí”

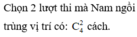
Trong 2 lượt đó, lượt đầu: Nam có 24 cách chọn vị trí, có 23! cách xếp vị trí cho 23 thí sinh còn lại; lượt sau: Nam có 1 cách chọn vị trí, có 23! cách xếp vị trí cho 23 thí sinh còn lại.