Cho tứ diện ABCD. Gọi M và N lần lượt là trung điểm của AB và CD. Mặt phẳng α qua MN cắt AD; BC lần lượt tại P và Q. Biết MP cắt NQ tại I. Ba điểm nào sau đây thẳng hàng?
A. I; A; C
B. I; B; D
C. I; A: B
D. I; C; D
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

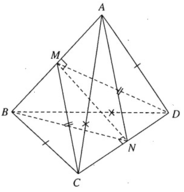
Hai tam giác ABC và BAD bằng nhau ( c.c.c) nên có các đường trung tuyến tương ứng bằng nhau: CM = DM
Ta có tam giác MCD cân tại M, do đó MN ⊥ CD vì N là trung điểm của CD. Tương tự ta chứng minh được NA = NB và suy ra MN ⊥ AB. Mặt phẳng (CDM) không vuông góc với mặt phẳng (ABN) vì (CDM) chứa MN vuông góc với chỉ một đường thẳng AB thuộc (ABN) mà thôi.

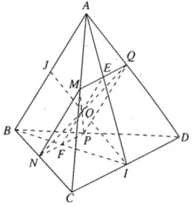
a) 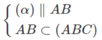
⇒ (α) ∩ (ABC) = MN và MN // AB
Ta có N ∈ (BCD) và 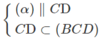
Nên ⇒ (α) ∩ (BCD) = NP và NP // CD
Ta có P ∈ (ABD)
Và 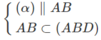 nên ⇒ (α) ∩ (ABD) = PQ và PQ // AB
nên ⇒ (α) ∩ (ABD) = PQ và PQ // AB
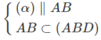 nên ⇒ (α) ∩ (ACD) = MQ và MQ // CD
nên ⇒ (α) ∩ (ACD) = MQ và MQ // CD
Do đó MN // PQ và NP // MQ, Vậy tứ giác MNPQ là hình bình hành.
b) Ta có: MP ∩ NQ = O. Gọi I là trung điểm của CD.
Trong tam giác ACD có : MQ // CD ⇒ AI cắt MQ tại trung điểm E của MQ.
Trong tam giác ACD có : NP // CD ⇒ BI cắt NP tại trung điểm F của NP.
Vì MNPQ là hình bình hành nên ta có
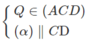
EF // MN ⇒ EF // AB
Trong ΔABI ta có EF // AB suy ra : IO cắt AB tại trung điểm J
⇒ I, O, J thẳng hàng
⇒ O ∈ IJ cố định.
Vì M di động trên đoạn AC nên Ochạy trong đoạn IJ .
Vậy tập hợp các điểm O là đoạn IJ.

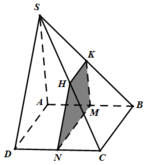

=> giao tuyến của (SCD) và (α) là NH// SD.
+ lại có HK là giao tuyến của (α) và (SBC) .
Thiết diện là tứ giác MNHK.
Ba mặt phẳng (ABCD) ; (SBC) và (α) đôi một cắt nhau theo các giao tuyến là MN; HK và BC mà MN// BC nên MN// HK. Vậy thiết diện là một hình thang .
Chọn B.

Chọn C
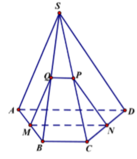
Giả sử mặt phẳng (P) cắt (SBC) theo giao tuyến PQ. Khi đo đó MN//BC nên theo định lý ba giao tuyến song song hoặc đồng quy áp dụng cho ba mặt phẳng (P);(SBC);(ABCD) thì ta được ba giao tuyến MN;BC;PQ đôi một song song. Do đó thiết diện là một hình thang.

Chọn C
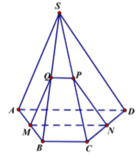
Giả sử mặt phẳng (P) cắt (SBC) theo giao tuyến PQ. Khi đo đó MN//BC nên theo định lý ba giao tuyến song song hoặc đồng quy áp dụng cho ba mặt phẳng (P);(SBC);(ABCD) thì ta được ba giao tuyến MN;BC;PQ đôi một song song. Do đó thiết diện là một hình thang.

Ta có CD ⊥ (ABN) (do BN ⊥ CD và AN ⊥ CD) ⇒ (BCD) ⊥ (ABN)
Đáp án C
Ta có giao tuyến của 2 mp (ABD) và (BCD) là BD.
Lại có I ∈ M P ⊂ A B D I ∈ N Q ⊂ B C D ⇒ I thuộc giao tuyến của (ABD) và (BCD).
=> I thuộc BD => 3 điểm I; B; D thẳng hàng.
Chọn B.