Cho hình chóp S.ABCD có đáy là hình bình hành tâm O, hai điểm M, N lần lượt là trung điểm của SB, SD; điểm P thuộc SC và không là trung điểm của SC. Gọi E là giao điểm của SO và MN; Q là giao điểm của SA và PE. Gọi F, G, H lần lượt là giao điểm của QM và AB, QP và AC, QN và AD. Tìm khẳng định đúng?
A. F nằm giữa G và H
B. 3 điểm F; G; H không thẳng hàng
C. G nằm giữa F và H
D. Tất cả sai

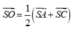
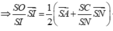
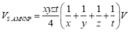
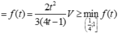
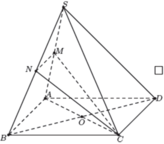
Từ (1) (2) và (3) suy ra ba điểm F, G, H thuộc giao tuyến của hai mặt phẳng (MNP) và (ABCD).
Do đó ba điểm F, G, H thẳng hàng và G nằm giữa F và H.
Chọn C.