Cho tứ diện ABCD có cạnh DA vuông góc với mặt phẳng (ABC) và AB=3 cm, BC=4 cm, A D = 6 c m , AC=5 cm. Khoảng cách từ A đến mặt phẳng (BCD) bằng
A. 12 5 cm
B. 12 7 cm
C. 6 cm
D. 6 10 cm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
28 tháng 3 2017
Đúng(0)
Những câu hỏi liên quan
CM
13 tháng 8 2019
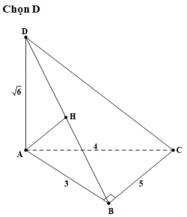
Đáp án A
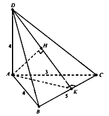
Vì B C 2 = B A 2 + A C 2 nên ∆ A B C vuông tại A.
Gọi K là hình chiếu của A lên BC, H là hình chiếu của A lên DK.
Ta có 1 A H 2 = 1 A D 2 + 1 A K 2 = 1 A D 2 + 1 A B 2 + 1 A C 2
= 1 4 2 + 1 4 2 + 1 3 2 = 17 72 ⇒ d A ; A B C D = A H = 72 17 = 12 34
CM
29 tháng 1 2019
Đáp án B
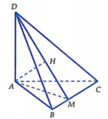
Ta có A B 2 + A C 2 = B C 2 ⇒ tam giác ABC vuông tại A.
Trong (ABC) kẻ AM vuông góc tại M ⇒ 1 A M 2 = 1 A B 2 + 1 A C 2
Trong (DAM) kẻ A H ⊥ D M tại H.
Ta có
D A ⊥ B C ; A M ⊥ B C ⇒ D A M ⊥ B C ⇒ D A M ⊥ D B C
D A M ⊥ D B C D A M ∩ D B C = D M A H ⊂ D A M ; A H ⊥ D M ⇒ A H ⊥ D B C
⇒ d A ; D B C = A H
Tam giác DAM vuông tại A có AH là đường cao
⇒ 1 A H 2 = 1 A M 2 + 1 A D 2 = 1 A B 2 + 1 A C 2 + 1 A D 2 = 1 3 2 + 1 4 2 + 1 4 2 = 17 72 ⇒ A H = 12 34
