Giải Chi Tiết Giúp Mình Với ạ !
Mình Hứa Sẽ Tick
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 2 2018
134/43 = 3,1162... bé - lớn : 55/21 ; 134/43 ; 116/37 ; 74/19
55/21 = 2,6190... lớn - bé : (ngược lại)
74/19 = 3,8947...
116/37 = 3,1351...
NH
0
NT
3
8 tháng 8 2017
\(A=45,98:0,01.4,2-6,27:0,5+3,9\)
\(A=\frac{4598}{100}:\frac{1}{100}.\frac{42}{10}-\frac{627}{100}:\frac{5}{10}+\frac{39}{10}\)
\(A=\frac{4598}{1000}.100.\frac{42}{10}-\frac{627}{100}.\frac{10}{5}+\frac{39}{10}\)
\(A=\frac{96558}{5}\)\(-\frac{627}{50}+\frac{39}{10}\)
\(A=\frac{965580}{50}-\frac{627}{50}+\frac{195}{50}=\frac{965148}{50}=19302,96\)
26 tháng 5 2021
Ta có
\(a^2+1=a^2+ab+bc+ca=a\left(a+b\right)+c\left(a+b\right)=\left(a+b\right).\left(a+c\right)\\ Cmtt:b^2+1=\left(b+a\right).\left(b+c\right)\\ c^2+1=\left(c+a\right).\left(c+b\right)\)
Nên
\(\dfrac{b-c}{a^2+1}+\dfrac{c-a}{b^2+1}+\dfrac{a-b}{c^2+1}\\ =\dfrac{\left(b-c\right)}{\left(a+b\right)\left(a+c\right)}+\dfrac{\left(c-a\right)}{\left(b+c\right)\left(b+a\right)}+\dfrac{\left(a-b\right)}{\left(c+a\right)\left(c+b\right)}\\ =\dfrac{\left(b-c\right)\left(b+c\right)+\left(c-a\right)\left(c+a\right)+\left(a-b\right)\left(a+b\right)}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}\\ =\dfrac{b^2-c^2+c^2-a^2+a^2-b^2}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}\\ =0\)
26 tháng 5 2021
\(\dfrac{b-c}{a^2+1}+\dfrac{c-a}{b^2+1}+\dfrac{a-b}{c^2+1}\)
\(=\dfrac{b-c}{a^2+ab+bc+ac}+\dfrac{c-a}{b^2+ab+bc+ca}+\dfrac{a-b}{c^2+ab+bc+ca}\)
\(=\dfrac{b-c}{a\left(a+b\right)+c\left(a+b\right)}+\dfrac{c-a}{b\left(a+b\right)+c\left(a+b\right)}+\dfrac{a-b}{c\left(c+a\right)+b\left(a+c\right)}\)
\(=\dfrac{b-c}{\left(a+c\right)\left(a+b\right)}+\dfrac{c-a}{\left(b+c\right)\left(a+b\right)}+\dfrac{a-b}{\left(b+c\right)\left(a+c\right)}\)
\(=\dfrac{\left(b-c\right)\left(b+c\right)+\left(c-a\right)\left(a+c\right)+\left(a-b\right)\left(a+b\right)}{\left(a+c\right)\left(a+b\right)\left(b+c\right)}\)
\(=\dfrac{b^2-c^2+c^2-a^2+a^2-b^2}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}=0\)
TL
1
Hứa Tick
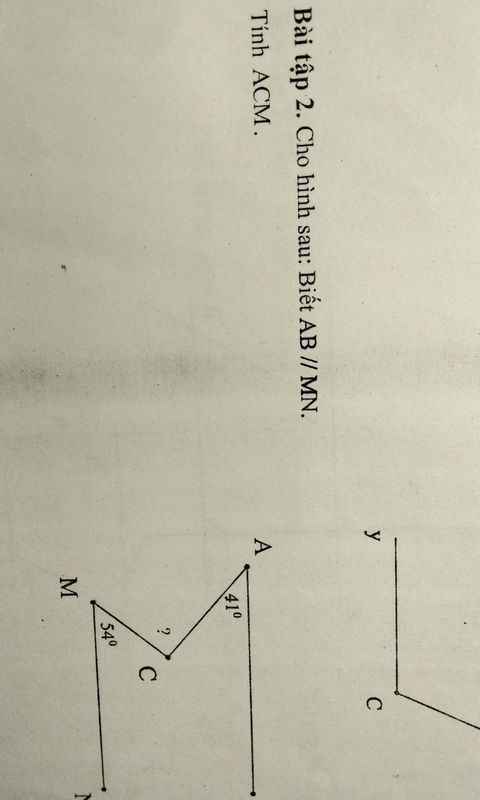
Kẻ CD//AB thì CD//MN
Do đó \(\widehat{ACD}=\widehat{CAB}=41^0;\widehat{MCD}=\widehat{CMN}=54^0\) (so le trong)
Vậy \(\widehat{ACM}=\widehat{ACD}+\widehat{DCM}=41^0+54^0=95^0\)