Từ các chữ số 1,3,5,7, 9 ta có thể lập được bao nhiêu số có ba chữ số khác nhau có tận cùng bằng 3 và nhỏ hơn 300
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 8 2019
Số lập được nhỏ hơn 50000 nên chữ số hàng chục nghìn phải là 3
Những số chẵn có năm chữ số khác nhau thoả mãn yêu cầu bài toán là: 35796, 35976, 37596, 37956, 39756, 39576
Vậy có thể lập được 6 số thoả mãn yêu cầu bài toán.
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 4 2023
Gọi số cần lập có dạng \(\overline{abc}\)
Do \(300< \overline{abc}< 500\Rightarrow a\) có 2 cách chọn (3 hoặc 4)
Bộ b, c có \(A_5^2=20\) cách chọn và hoán vị
\(\Rightarrow2.20=40\) số thỏa mãn
VH
2
BD
31 tháng 10 2016
Ta có :
1 cách chọn hàng đơn vị
4 cách chọn hàng phần mười
3 cách chọn hàng phần trăm
2 cách chọn hàng phần nghìn
Theo quy tắc nhân ta có :
1 x 4 x 3 x 2 = 24 ( số )
đ/s : 24 số
31 tháng 10 2016
CÓ:
1 cách chọn chữ số phần nguyên
4 cách chọn chữ số hàng phần mười
3 cách chọn chữ số hàng phần trăm
2 cách chọn chữ số hàng phần nghìn
VẬY CÓ TẤT CẢ SỐ CÁC SỐ DÃ LẬP ĐC LÀ 1.2.3.4=24 số
Đ/S:24 số
BC
2
20 tháng 1 2023
\(\overline{abc}\)
a có 3 cách chọn
b có 5 cách chọn
c có 4 cách chọn
=>Có 3*4*5=60 số
H
20 tháng 1 2023
Gọi ba chữ số cần tìm là : \(\overline{abc}\)
\(+,TH1:a=3\)
=> a có 1 cách chọn
\(b,c\) có \(A_5^2\) cách chọn
\(=>\) số t/m là : \(1.A_5^2=20\left(số\right)\)
\(+,TH2:a\in\left\{4;5\right\}\)
=> a có \(2\) cách chọn
\(b,c\) có \(A_5^2\) cách
\(=>\) số t/m là : \(2\times A_5^2=40\left(số\right)\)
=> SỐ CẦN TÌM LÀ : \(20+40=60\left(số\right)\)
CM
31 tháng 7 2018
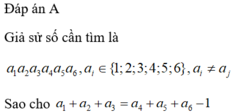
Vậy số cách để lập số có 6 chữ số khác nhau sao cho tổng ba số đầu nhỏ hơn tổng ba số cuối một đơn vị là: 
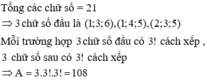
Từ các chữ số 1,3,5,7,9 ta có thể lập được bao nhiêu số có bốn chữ số khác nhau có tận cùng bằng 3 và nhỏ hơn 3000
Số cần tìm nhỏ hơn 300 nên chữ số hàng trăm là 1
Các số thoả mãn yêu cầu bài toán là 1573, 1593, 1753, 1793, 1953, 1973
Vậy ta lập được tất cả là 6 số