Cho tam giác ABC có diện tích 12 c m 2 . Gọi N là trung điểm của BC, M trên AC sao cho AM = 1 3 AC, AN cắt BM tại O.
Khẳng định nào sau đây là đúng nhất?
A. AO = ON
B. BO = 3OM
C. BO < 3OM
D. Cả A, B đều đúng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
6 tháng 5 2017
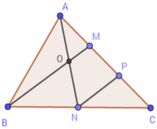
Lấy P là trung điểm của CM.
Vì AM = 1 3 AC => MC = 2 3 AC => MP = PC = 1 3 AC = AM
Tam giác BCM có: N B = N C ( g t ) P C = P M ( g t )
Suy ra NP là đường trung bình của tam giác BMC (định nghĩa).
Suy ra NP // BM (tính chất đường trung bình).
Tam giác ANP có: M A = M P ( c m t ) O M / / N P ( d o N P / / B M )
=> AO =ON (định lý đảo của đường trung bình).
Theo chứng minh trên ta có OM là đường trung bình của tam giác ANP nên OM = 1 2 NP (1)
NP là đường trung bình của tam giác BCM nên NP = 1 2 BM (2)
Từ (1) và (2) suy ra BM = 4OM => BO = 3OM
Vậy cả A, B đều đúng
Đáp án cần chọn là: D
CM
29 tháng 3 2018
Hai tam giác AOM và ABM có chung đường cao hạ từ A
nên = S A O M S A B M = O M B M = 1 4
=> SAOM = 1 4 SABM
Hai tam giác ABM và ABC có chung đường cao hạ từ B
nên S A B M S A B C = A M A C = 1 3
=> SABM = 1 3 SABC
Vậy SAOM = 1 4 . 1 3 .12 = 1 (cm2)
Đáp án cần chọn là: D
Lấy P là trung điểm của CM.
Tam giác BCM có: N B = N C ( g t ) P C = P M ( g t )
suy ra NP là đường trung bình của tam giác BMC (định nghĩa). Suy ra NP // BM (tính chất đường trung bình).
Tam giác ANP có M A = M P ( g t ) O M / / N P ( d o N P / / B M )
=> AO = ON (định lý đảo của đường trung bình).
Ta có OM là đường trung bình của tam giác ANP (cmt) nên OM = 1 2 NP (1)
NP là đường trung bình của tam giác BCM nên NP = 1 2 BM (2)
Từ (1) và (2) suy ra BM = 4OM => BO = 3OM.
Vậy AO = ON; BO = 3OM.
Đáp án cần chọn là: D