Cho hình lăng trụ đứng đáy là hình thoi có hai đường chéo lần lượt là 8cm và 10cm. Tính chiều cao của lăng trụ đứng biết thể tích của lăng trụ đứng là 360 c m 3 .
A. 18cm
B. 12cm
C. 9cm
D. 10cm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



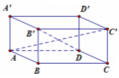
Gọi O là giao điểm 2 đường chéo AC và BD.
Vì AC=8 cm, BD=6cm
\(\Rightarrow\)OA=4cm, OB=3cm\(\Rightarrow\)AB=5cm
Chu vi đáy: 2p=5.4=20 (cm)
\(S_{xq}=20\cdot7=170\left(cm^2\right)\)
\(S_{đáy}=\frac{AC\cdot BD}{2}=\frac{8\cdot6}{2}=24\left(cm^2\right)\)
\(\Rightarrow V=S_{đáy}\cdot h=24\cdot7=168\left(cm^3\right)\)

Đáp án D
Ta dễ dàng tính được
![]()
Xét hình bình hành A’B’C’D’, ta dễ dàng tính được diện tích đáy S = 3 2 a 2
Suy ra thể tích khối lăng trụ đứng là:
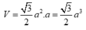
=> Chọn phương án D

Đáp án A
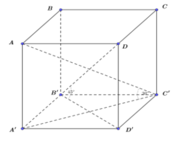
D B ' , A B C D ^ = B D B ' ^ = 60 ° ⇒ B D = B B ' 3 = 2 3 A C ' , A B C D ^ = C A C ' ^ = 60 ° ⇒ A C = C C ' = 2
Áp dụng định lí Cosi ta có:
A B 2 + A D 2 − 2 A B . A D cos B A D ^ = B D 2 A B 2 + A D 2 − 2 A B . A D cos A B C ^ = A C 2 ⇔ A B 2 + A D 2 − 2 A B . A D 2 = 4 3 A B 2 + A D 2 + 2 A B . A D 2 = 4 ⇒ A B . A D = 2 2 3 ⇒ V S . A B C D = 2 S A B D = A B . A D . sin B A D ^ = 2 3 ⇒ V A B C D . A ' B ' C ' D ' = S A B C D . A A ' = 4 3

vì 2 đường chéo của hình thoi vuông góc với nhau và cắt nhau tại trung điểm mỗi đường nên 1 nửa cả 2 đường chéo lần lượt là 3 và 4
vì vuông góc dùng định lý pitago tích cạnh của hình thoi \(\sqrt{3^{2}+4^{2}}=5\)cm
Stp=Sđáy+Sxq
248= 1/2.6.8+5.4.h
=> h=11,2
thể tích hình lăng trụ 6.8.11,2:2=268.8 (tại bạn ko cho đv ban đầu nên mk ko để đv nhé)