Question

[Pham Trong Bach]

Một người vay ngân hàng 500 triệu đồng với lãi suất 0,5% trên 1 tháng. Theo thỏa thuận cứ mỗi tháng người đó sẽ trả cho ngân hàng 10 triệu đồng và cứ trả hàng tháng như thế cho đến khi hết nợ (tháng cuối cùng có thể trả dưới 10 triệu). Hỏi sau bao nhiêu tháng thì người đó trả được hết nợ ngân hàng.

A. 57

B. 56

C. 58

D. 69

Answer 1

[Cao Minh Tâm]

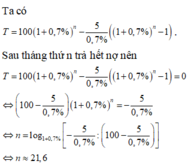
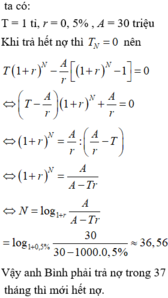
Đáp án C

Phương pháp giải: Áp dụng công thức bài toán vay vốn trả góp, hoặc tìm từng tháng, dùng phương pháp quy  nạp và đưa về tổng của cấp số nhân

Lời giải:

Sau tháng thứ nhất số tiền gốc còn lại trong ngân hàng là 500(1+0,5%) - 10 triệu đồng.

Sau tháng thứ hai số tiền gốc còn lại trong ngân hàng là

[500(1+0,5%) – 10].(1+0,5%) – 10 = 500.(1+0,5%)² – 10[(1+0,5%)+1] triệu đồng

Sau tháng thứ ba số tiền gốc còn lại trong ngân hàng là

500.(1+0,5%)³ – 10[(1+0,5%)² + (1+0,5%) +1] triệu đồng

Số tiền gốc còn lại sau tháng thứ  n là

500(2+0,5%)ⁿ – 10[(1+0,5%)^n-1 + (1+0,5%)^n-2 + … + 1] triệu đồng

Đặt y = 1+0,5% = 1,005 thì ta có số tiền gốc còn lại trong ngân hàng sau tháng thứ  n là

Vì lúc này số tiền cả gốc lẫn lãi đã trả hết

Vậy sau 58 tháng thì người đó trả hết nợ ngân hàng