Cho tam giác ABC nhọn,đường tròn tâm O,đường kính BC cắt 2 cạnh AB,AC lần lượt tại M và N.Gọi H là giao điểm của BN và CM
a)Chứng minh AH vuông góc với BC
b) Chứng minh MN<BC
c)Gọi I là trung điểm MN.Chứng minh OI vuông góc với MN
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 1 2023
nếu bạn làm được thì bạn hãy làm đi , tra mạng , và tham khảo ít thôi nhé
1 tháng 1 2023
Xét (O) có
ΔBMC nội tiếp
BC là đường kính
Do đó: ΔBMC vuông tại M
Xét (O) có
ΔBNC nội tiếp
BC là đường kính
Do đo: ΔBNC vuông tại N
Xet ΔABC có
BN,CM là các đường cao
BN cắt CM tại H
Do đó; H là trực tâm
=>AH vuông góc với BC
21 tháng 8 2022
a: Xét (O) có
ΔBFC nội tiếp
BC là đường kính
Do đó: ΔBFC vuông tại F
Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
Xét ΔABC có
BE,CF là đường cao
BE cắt CF tại H
Do đó: AH vuông góc với BC tại D
b:
Xét tứ giác CDFA có góc CDA=góc CFA=90 độ
nên CDFA là tứ giác nội tiếp
=>góc BFD=góc BCA
Xét tứ giác BFEC có góc BFC=góc BEC=90 độ
nên BFEC là tứ giác nội tiếp
=>góc AFE=góc ACB
Ta có: góc COE=180 độ-2 góc C
góc EFD=180 độ-góc AFE-góc BFD
=180 độ-2 góc C
=>góc COE=góc EFD
=>DOEF là tứ giác nội tiếp
22 tháng 2 2022
a: Xét (O) có
ΔMBC nội tiếp
BC là đường kính
Do đó: ΔMBC vuông tại M
Xét (O) có
ΔNBC nội tiếp
BC là đường kính
Do đó:ΔNBC vuông tại N
Xét ΔABC có
BN là đường cao
CM là đường cao
BN cắt CM tại H
Do đó: AH⊥BC tại K
b: Xét ΔANB vuông tại N và ΔAMC vuông tại M có
\(\widehat{MAC}\) chung
Do đó: ΔANB∼ΔAMC
Suy ra: AN/AM=AB/AC
hay \(AN\cdot AC=AB\cdot AM\)
CM
17 tháng 2 2018
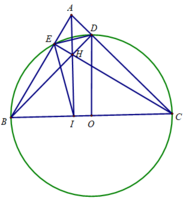
a) Chứng minh AI BC
Ta có ∠BEC = BDC = 90 0 (hai góc nội tiếp chắn nửa đườn tròn)
30 tháng 9 2021
a: Xét (O) có
ΔBMC nội tiếp đường tròn
BC là đường kính
Do đó: ΔBMC vuông tại M
Xét (O) có
ΔBNC nội tiếp đường tròn
BC là đường kính
Do đó: ΔBNC vuông tại N
Xét ΔBAC có
BN là đường cao ứng với cạnh huyền AC
CM là đường cao ứng với cạnh huyền AB
BN cắt CM tại H
Do đó: AH⊥BC
a: Xét (O) có
ΔBNC nội tiếp đường tròn
BC là đường kính
Do đó: ΔBNC vuông tại N
Xét (O) có
ΔBMC nội tiếp đường tròn
BC là đường kính
Do đó: ΔBMC vuông tại M
Xét ΔABC có
BN là đường cao
CM là đường cao
BN cắt CM tại H
Do đó: AH\(\perp\)BC