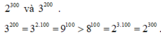so sanh: 2^300+3^300+4^300 và 729 . 24^100
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KH
0
CM
6 tháng 2 2017
2300 = (23)100 = 8100 và 3200 = (32)100 = 9100 nên 2300 < 3200;
KN
16 tháng 2 2020
Ta có: \(A=\left[6.\left(\frac{-1}{3}\right)^2-\left(-\frac{1}{3}\right)+1\right]:\left(\frac{-1}{3}-1\right)\)
\(\Rightarrow A=\left[6.\frac{1}{9}+\frac{1}{3}+1\right]:\left(\frac{-1}{3}-\frac{3}{3}\right)\)
\(\Rightarrow A=\left[\frac{2}{3}+\frac{1}{3}+1\right]:\frac{-4}{3}\)
\(\Rightarrow A=\left[1+1\right].\frac{-3}{4}=2.\frac{-3}{4}=\frac{-3}{2}\)
Mà \(B=\left(729-1^3\right)\left(729-2^3\right)\left(729-3^3\right)...\left(729-125^3\right)\)
\(=\left(729-1^3\right)\left(729-2^3\right)...\left(729-9^3\right)...\left(729-125^3\right)\)
\(=\left(729-1^3\right)\left(729-2^3\right)...0...\left(729-125^3\right)=0\)
Vì \(\frac{-3}{2}< 0\)nên A < B
NV
3
23 tháng 9 2016
\(\text{So Sánh: 9^21 và 729^7}\)
\(9^{21}\text{ giữ nguyên}\)
\(729^7=\left(9^3\right)^7=9^{3.7}=9^{21}\)
Vì \(9^{21}=9^{21}\text{ nên }9^{21}=729^7\)
23 tháng 9 2016
Ta có: 921 = (32)21 = 342 (1)
7297 = (36)7 = 342 (2)
Từ 1 và 2 ta có 342 = 342 => 921 = 7297
LQ
16 tháng 6 2016
2 cuốn a + 5 cuốn b =15500 đồng
3 cuốn a - 2 cuốn b = 3300 đồng.
Dùng thử giả thuyết tạm, giờ mình bận rồi, cm cho mình , mình sẽ giải cho. Lê Quang Thế.
LQ
16 tháng 6 2016
2 cuốn a + 5 cuốn b = 15500 đồng
3 cuốn a - 2 cuốn b = 3300 đồng
Làm cho 2 biểu thức này có số cuốn a giống nhau
6 cuốn a + 15 cuốn b = 15500 x 3 = 46500 đồng
6 cuốn a - 4 cuốn b = 3300 x 2 = 6600 đồng
6 cuốn a = 4 cuốn b + 6600 đồng
(4 cuốn b + 6600 đồng) + 15 cuốn b = 46500 đồng
19 cuốn b = 46500 - 6600 = 39900
cuốn b = 2100
Tự tìm cuốn a nhé
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
21 tháng 10 2021
\(2^{300}+3^{300}+4^{300}-729.24^{100}=\)
\(=2^{300}+3^{300}+\left(2^2\right)^{300}-3^6.\left(2^3.3\right)^{100}=\)
\(=2^{300}+3^{300}+2^{600}-2^{300}.3^{106}=\)
\(=2^{300}\left(1+2^{300}-3^{106}\right)+3^{300}\)
Ta có
\(2^{300}=\left(2^2\right)^{150}=4^{150}>3^{150}>3^{106}\Rightarrow2^{300}-3^{106}>0\)
\(\Rightarrow2^{300}\left(1+2^{300}-3^{106}\right)+3^{300}>0\)
\(\Rightarrow2^{300}+3^{300}+4^{300}>729.24^{100}\)
