Cho góc xOy là góc tù. Trên nửa mặt phẳng chứa tia Ox có bờ chứa tia Oy, vẽ tia Oy' vuông góc với Oy. Trên nửa mặt phẳng chứa tia Oy có bờ chứa tia Ox vẽ Õ' vuông góc với Ox
a) Chứng minh góc xOy'=x'Oy'
b) Góc xOy và góc xOy'có cùng một tia phân giác
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 8 2017
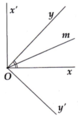
Ta có: x O y ^ + x ' O y ^ = 90° và x O y ^ + x O y ' ^ = 90° => x ' O y ^ = x O y ' ^ .
Mặt khác Ox', Oy' nằm trên hai nửa mặt phẳng đối nhau bờ Ox nên Ox nằm giữa hai tia Ox' và Oy'.
Tương tự Oy nằm giữa hai tia Ox' và Oy'
Gọi Om là phân giác góc xOy, suy ra Oy
nằm giữa Ox' và Om, Ox nằm giữa Oy' và
Om, Om nằm giữa Ox và Oy.
Lại có Om là phân giác góc xOy
=> x O m ^ = y O m ^ và x ' O y ^ = x O y ' ^ (cùng phụ x O y ^ ). Do đó x ' O m ^ = y ' O m ^ .
=> Om cũng là phân giác của x ' O y ' ^ (ĐPCM)
CM
15 tháng 8 2019
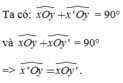
Mặt khác Ox', Oy' nằm trên hai nửa mặt phẳng đối nhau bờ Ox nên Ox nằm giữa hai tia Ox' và Oy'.
Tương tự Oy nằm giữa hai tia Ox' và Oy'
Gọi Om là phân giác góc xOy, suy ra Oy nằm giữa Ox' và Om, Ox nằm giữa Oy' và Om, Om nằm giữa Ox và Oy.
1 tháng 7 2019
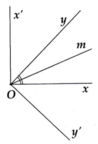
a) Ta có :
xOy' + y'Ox' =90 độ (gt)
y'Ox' + x'Oy = 90 độ (gt)
=> xOy' = 90 - y'Ox'
=> x'Oy = 90 - y'Ox'
=> xOy' = x'Oy (cùng bằng 90 - y'Ox')(dpcm)
1 tháng 7 2019
b) Gọi Ot là pg y'Ox'(1)
=> y'Ot = x'Ot
tOy = tOx' + x'Oy
Mà y'Ot = tOx'
xOy' = x'Oy (cmt)
=> xOt = tOy
=> Ot là pg xOy (2)
Từ (1) và (2) ta có :
=> y'Ox' và xOy có cùng tia pg
