Tính nhahh : 4 × 5 - 40 : 4 × 2 / 128 : 8 × 16 × ( 4 + 52 : 4 )
Tìm 10 số hạng đầu tiên của dãy : 1/2 + 1/6 + 1/12 + 1/20 + 1/30 +...
Tổng 2 số là 60. Biết 1/2 số thứ nhất hơn 1/8 số thứ hai là 5 . Tìm mỗi số
Giải nhanh hộ mình với><♡
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
B1
26 tháng 8 2017
1. Phương pháp 1: ( Hình 1)
Nếu 
thì ba điểm A; B; C thẳng hàng.
2. Phương pháp 2: ( Hình 2)
Nếu AB // a và AC // a thì ba điểm A; B; C thẳng hàng.
(Cơ sở của phương pháp này là: tiên đề Ơ – Clit- tiết 8- hình 7)
3. Phương pháp 3: ( Hình 3)
Nếu AB 
a ; AC A thì ba điểm A; B; C thẳng hàng.
( Cơ sở của phương pháp này là: Có một và chỉ một đường thẳng
a’ đi qua điểm O và vuông góc với đường thẳng a cho trước
- tiết 3 hình học 7)
Hoặc A; B; C cùng thuộc một đường trung trực của một
đoạn thẳng .(tiết 3- hình 7)
4. Phương pháp 4: ( Hình 4)
Nếu tia OA và tia OB là hai tia phân giác của góc xOy
thì ba điểm O; A; B thẳng hàng.
Cơ sở của phương pháp này là:
Mỗi góc có một và chỉ một tia phân giác .
* Hoặc : Hai tia OA và OB cùng nằm trên nửa mặt phẳng bờ chứa tia Ox , 
thì ba điểm O, A, B thẳng hàng.
5. Nếu K là trung điểm BD, K’ là giao điểm của BD và AC. Nếu K’
Là trung điểm BD thì K’ 
K thì A, K, C thẳng hàng.
(Cơ sở của phương pháp này là: Mỗi đoạn thẳng chỉ có một trung điểm)
C. Các ví dụ minh họa cho tùng phương pháp:
Phương pháp 1
Ví dụ 1. Cho tam giác ABC vuông ở A, M là trung điểm AC. Kẻ tia Cx vuông góc CA
(tia Cx và điểm B ở hai nửa mặt phẳng đối nhau bờ AC). Trên tia Cx lấy điểm
D sao cho CD = AB.
Chứng minh ba điểm B, M, D thẳng hàng.
Gợi ý: Muốn B, M, D thẳng hàng cần chứng minh 
Do 
nên cần chứng minh 
BÀI GIẢI:
AMB và CMD có: 
AB = DC (gt).
MA = MC (M là trung điểm AC)
Do đó: AMB = CMD (c.g.c). Suy ra:
Mà (kề bù) nên .
Vậy ba điểm B; M; D thẳng hàng.
Ví dụ 2. Cho tam giác ABC. Trên tia đối của AB lấy điểm D mà AD = AB, trên tia đối
tia AC lấy điểm E mà AE = AC. Gọi M; N lần lượt là các điểm trên BC và ED
sao cho CM = EN.
Chứng minh ba điểm M; A; N thẳng hàng.
Gợi ý: Chứng minh 
từ đó suy ra ba điểm M; A; N thẳng hàng.
BÀI GIẢI (Sơ lược)
ABC = ADE (c.g.c) 
ACM = AEN (c.g.c) 
Mà 
(vì ba điểm E; A; C thẳng hàng) nên
Vậy ba điểm M; A; N thẳng hàng (đpcm)
BÀI TẬP THỰC HÀNH CHO PHƯƠNG PHÁP 1
Bài 1: Cho tam giác ABC. Trên tia đối của tia AB lấy điểm D sao cho AD = AC, trên tia đối
của tia AC lấy điểm E sao cho AE = AB. Gọi M, N lần lượt là trung điểm của BE và
CD.
Chứng minh ba điểm M, A, N thẳng hàng.
Bài 2: Cho tam giác ABC vuông ở A có 
. Vẽ tia Cx BC (tia Cx và điểm A ở
phía ở cùng phía bờ BC), trên tia Cx lấy điểm E sao cho CE = CA. Trên tia đối của tia
BC lấy điểm F sao cho BF = BA.
Chứng minh ba điểm E, A, F thẳng hàng.
Bài 3: Cho tam giác ABC cân tại A, điểm D thuộc cạnh AB. Trên tia đối của tia CA lấy điểm
E sao cho CE = BD. Kẻ DH và EK vuông góc với BC (H và K thuộc đường thẳng BC)
Gọi M là trung điểm HK.
Chứng minh ba điểm D, M, E thẳng hàng.
Bài 4: Gọi O là trung điểm của đoạn thẳng AB. Trên hai nửa mặt phẳng đối nhau bờ AB, kẻ
Hai tia Ax và By sao cho 
.Trên Ax lấy hai điểm C và E(E nằm giữa A và C),
trên By lấy hai điểm D và F ( F nằm giữa B và D) sao cho AC = BD, AE = BF.
Chứng minh ba điểm C, O, D thẳng hàng , ba điểm E, O, F thẳng hàng.
Bài 5.Cho tam giác ABC . Qua A vẽ đường thẳng xy // BC. Từ điểm M trên cạnh BC, vẽ các
đường thẳng song song AB và AC, các đường thẳng này cắt xy theo thứ tự tại D và E.
Chứng minh các đường thẳng AM, BD, CE cùng đi qua một điểm.
PHƯƠNG PHÁP 2
Ví dụ 1: Cho tam giác ABC. Gọi M, N lần lượt là trung điểm của các cạnh AC, AB. Trên
Các đường thẳng BM và CN lần lượt lấy các điểm D và E sao cho M là trung
điểm BD và N là trung điểm EC.
Chứng minh ba điểm E, A, D thẳng hàng.
Hướng dẫn: Xử dụng phương pháp 2
Ta chứng minh AD // BC và AE // BC.
BÀI GIẢI.
BMC và DMA có:
MC = MA (do M là trung điểm AC)
(hai góc đối đỉnh)
MB = MD (do M là trung điểm BD)
Vậy: BMC = DMA (c.g.c)
Suy ra: 
, hai góc này ở vị trí so le trong nên BC // AD (1)
Chứng minh tương tự : BC // AE (2)
Điểm A ở ngoài BC có một và chỉ một đường thẳng song song BC nên từ (1)
và (2) và theo Tiên đề Ơ-Clit suy ra ba điểm E, A, D thẳng hàng.
Ví dụ 2: Cho hai đoạn thẳng AC và BD cắt nhau tai trung điểm O của mỗi đoạn. Trên tia
AB lấy lấy điểm M sao cho B là trung điểm AM, trên tia AD lấy điểm N sao cho
D là trung điểm AN.
AH
Akai Haruma
Giáo viên
27 tháng 6 2021
Lời giải:
Coi $x$ là số hạng thứ 2014. Bạn nhớ công thức tìm số số hạng như sau:
$(x-2):2+1=2014$
Như vậy đương nhiên số hạng thứ 2014 là:
$x=(2014-1)\times 2+2$
Số 1 có ý nghĩa như vậy.
CT
6 tháng 10 2021
Dãy a) với b) không có quy luật
c) 3 + 6 + 9 + ... + 147
Khoảng cách là : 3
Số số hạng là:
( 147 - 3 ) / 3 + 1 = 49 ( số hạng )
Tổng trên là:
( 147 + 3 ) * 49 / 2 = 3675
Đ/s: c) 3675
CT
6 tháng 10 2021
a/số chia cho 5 dư 1 thì có tận cùng là 1 hoặc 6; vậy có số số chia cho 5 dư 1 là:
(996-101): 5 +1=180(số) số chia cho 5 dư 2 thì có tận cùng là 2 hoặc 7; vậy có số số chia cho 5 dư 2 là:
(997-102): 5+1=180(số)
b/Số số có 4 chữ số chia hết cho 3 là:
(9999-1002):3+1=3000(số)
c/Số số có 3 chữ số <500 mà chia hết cho 4 là:
(496-100):4+1=100(số)
18 tháng 9 2017
Tổng 2 số lẻ là 98 , tìm lớn biết giữa chúng có 6 số chẵn ?
bài làm
vì giữa chúng có 4 số chẵn mà mỗi số chẵn cách nhau hai đơn vị nên giữa 2 số lẻ cách nhau: 2x4=8
ta có bài toán tổng hiệu
tổng=98 và hiệu=8
số chẵn thứ nhất
(98-8):2=45
số chẵn thứ hai
(98+8):2=53
đáp số: 45; 53
Tìm 1 số khi biết nếu lấy số đó chia 8 dư 5 , chia 12 dư 1 và hai thương kém nhau 3 đơn vị ?
OM
18 tháng 9 2017
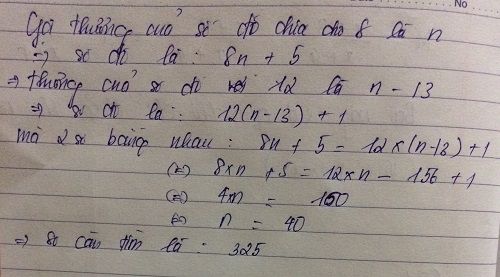
Câu1
Bài làm
Ta có: 2/5 số thứ nhất = 1/4 số thứ hai = 4/15 số thứ 3
<=> 4/10 số thữ nhất = 4/16 số thứ hai = 4/15 số thứ 3
=> Số thứ nhất chiếm 10 phần
Số thứ hai chiếm 16 phần
Số thứ 3 chiếm 15 phần
Tổng số phần bằng nhau là:
10 + 15 + 16 = 41(phần)
Số thứ nhất là:
410 : 41 x 10 = 100
Số thứ hai là:
410 : 41 x 15 = 150
Số thứ ba là:
410 : 41 x 16 = 191
Đs:...
