Cho đoạn thẳng AB. Gọi d là đường trung trực của AB. Trên đường thẳng d lấy điểm M bất kì. Trong mặt phẳng lấy điểm C sao cho BC< CA
,Tìm vị trí của M trên d sao cho MB+MC nhỏ nhất
Mấy pro giúp cái coi :>
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

M thuộc d nên MA = MB. Vậy MB + MC = MA + MC. Trong tam giác MAC, ta có : MA + MC > AC. Vậy MB + MC > AC
Vì CB < CA nên C và B nằm trong cùng một nửa mặt phẳng bờ d. Do đó A và C nằm trong hai nửa mặt phẳng bờ d khác nhau. Do đó d cắt AC tại H.
Vậy khi M ≡≡ H thì : MB + MC = HB + HC = HA + HC
=> MB + MC = AC
Vậy ta có MB + MC ≥ AC
Khi M trùng với H thì HB + HC = AC.
Tức là MB + MC nhỏ nhất khi M ≡≡ H giao điểm của AC với d.

M thuộc d nên MA = MB. Vậy MB + MC = MA + MC. Trong tam giác MAC, ta có : MA + MC > AC. Vậy MB + MC > AC
Vì CB < CA nên C và B nằm trong cùng một nửa mặt phẳng bờ d. Do đó A và C nằm trong hai nửa mặt phẳng bờ d khác nhau. Do đó d cắt AC tại H.
Vậy khi M ≡≡ H thì : MB + MC = HB + HC = HA + HC
=> MB + MC = AC
Vậy ta có MB + MC ≥ AC
Khi M trùng với H thì HB + HC = AC.
Tức là MB + MC nhỏ nhất khi M ≡≡ H giao điểm của AC với d

M thuộc d nên MA = MB. Vậy MB + MC = MA + MC. Trong tam giác MAC, ta có : MA + MC > AC. Vậy MB + MC > AC
Vì CB < CA nên C và B nằm trong cùng một nửa mặt phẳng bờ d. Do đó A và C nằm trong hai nửa mặt phẳng bờ d khác nhau. Do đó d cắt AC tại H.
Vậy khi M ≡≡ H thì : MB + MC = HB + HC = HA + HC
=> MB + MC = AC
Vậy ta có MB + MC ≥ AC
Khi M trùng với H thì HB + HC = AC.
Tức là MB + MC nhỏ nhất khi M ≡≡ H giao điểm của AC với d

Câu 1 :
a) Xét \(\Delta ABC\) cân tại A mà AI là phân giác
\(\Rightarrow\) AI là trung tuyến ; AI là đường cao
\(\Rightarrow\) \(AI\perp BC\)
b) Xét \(\Delta ABC\) có AI ; CM lần lượt là trung tuyến cuả BC và AB và G là giao điểm của CM và AI
\(\Rightarrow\) G là trọng tâm \(\Delta ABC\) \(\Rightarrow\) BG là trung tuyến của \(\Delta ABC\)
c) Có AI là trung tuyến \(\Rightarrow BI=CI=\frac{BC}{2}=\frac{18}{2}=9cm\)
Xét \(\Delta ABI\) vuông tại I
\(\Rightarrow AB^2=AI^2+IB^2\Rightarrow AI^2=AB^2-BI^2\Rightarrow AI=12cm\)
Vì G là trọng tâm \(\Delta ABC\) \(\Rightarrow\) \(GI=\frac{1}{3}AI\Rightarrow GI=\frac{1}{3}12=4cm\)

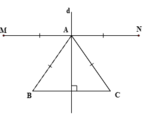
Ta có: B A M ^ = B ^ ( g t ) C A N ^ = C ^ ( g t )
Þ AM // BC; AN // BC (vì có cặp góc so le trong bằng nhau).
Þ 3 điểm M, A, N thẳng hàng (vì qua điểm A chỉ vẽ được một đường thẳng song song với BC).
Vậy MN // BC mà d ⊥ B C nên d ⊥ M N (1)
Ta có: A M = A B ; A N = A C
mà AB = AC (gt) nên AM = AN. (2)
Từ (1) và (2) Þ d là trung trực của MN
M thuộc d nên MA = MB. Vậy MB + MC = MA + MC. Trong tam giác MAC, ta có : MA + MC > AC. Vậy MB + MC > AC
Vì CB < CA nên C và B nằm trong cùng một nửa mặt phẳng bờ d. Do đó A và C nằm trong hai nửa mặt phẳng bờ d khác nhau. Do đó d cắt AC tại H.
Khi M trùng với H thì HB + HC = AC.
Tức là MB + MC nhỏ nhất khi M ≡≡ H giao điểm của AC với d.