Cho hình bình hành ABCD AB lớn hơn Ad trên cạnh AB lấy điểm M tùy ý sao cho AM lớn hơn MB và m không trùng với điểm A ,B đường thẳng mc kéo dài cắt ad tại N đường thẳng Nb cắt dC tại p Chứng minh tam giác ndc đồng dạng với tam giác cbm và chứng minh pc.pn=pb.pd và nối bd cắt nc tại e chứng minh ce^2= em.en
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 8 2019
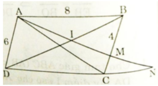
a) AD // BC (gt)
b) Xét ΔAMB và ΔNAD có:
∠BAM = ∠ AND (so le trong, AB // CD)
∠ABM = ∠ADN (góc đối của hình bình hành)
⇒ ΔAMB ∼ ΔNAD (g.g)
c) ΔAMB ∼ ΔNAD (cmt)
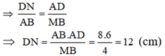
Do đó: CN = DN – DC = 12 – 8 = 4 (cm)
d) Do AB //CD nên theo hệ quả định lí Ta-lét, ta có
Tương tự, do AD // BM nên
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 3 2023
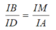
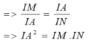
Đề sai rồi, em kiểm tra lại, EK, HF và BD ko hề đồng quy
MA
10 tháng 3 2023
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB < MD. Đường thẳng qua M và song song với AB cắt AD và BC lần lượt tại E và F. Đường thẳng qua M song song với AD cắt AB và AC lần lượt tại K và H.
1. Chứng minh: các đường thẳng EK, HF, BD đồng quy
2. Cho SMKF = 9 cm2 ; SMEH = 25 cm2 . Tính SABCD.
