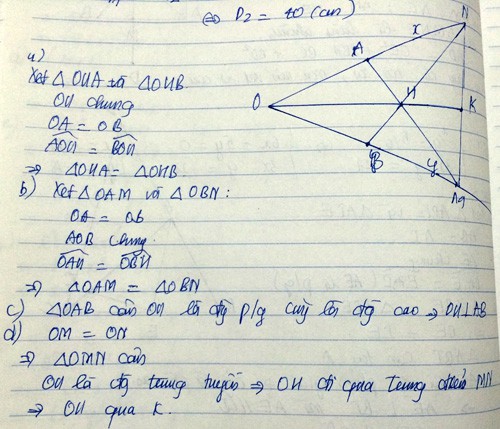
Cho điểm A thuộc tia phân giác của góc vuông xOy. Gọi D, E lần lượt là hình chiếu vuông góc của điểm A trên hai cạnh Ox, Oy. Trên đoạn OD lấy điểm M. Đường vuông góc với AM tại A cắt tia Oy ở n. Gọi H, I theo thứ tự là giao điểm của DE với MA và MN.
a, ΔAMN là tam giác gì? Vì sao?
b, Chứng minh : AI ⊥ MN.
c, Gọi K là trung điểm của AN. Chứng minh OH // EK.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

16 tháng 5 2022
a: Ta có: ΔOAB cân tại O
mà OI là đường phân giác
nên OI là đường cao
b: XétΔOAB có
OI là đường cao
AD là đường cao
OI cắt AD tại C
Do đó: C là trực tâm của ΔOAB
Suy ra: BC\(\perp\)Ox
c: Xét ΔOAB cân tại O có \(\widehat{AOB}=60^0\)
nên ΔOAB đều
=>\(OC=\dfrac{2}{3}OI=\dfrac{2}{3}\cdot\dfrac{a\sqrt{3}}{2}=\dfrac{2}{3}\cdot\dfrac{6\sqrt{3}}{2}=2\sqrt{3}\left(cm\right)\)