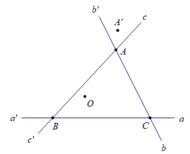
Cho nửa (O;R) đường kính AB . Kẻ tiếp tuyến Ax với nửa đường tròn đó ( tia Ax thuộc nửa mặt phẳng bờ chứa nửa (O) ). Từ điểm M bất kỳ trên tia Ax kẻ tiếp tuyến thứ 2 MC với nửa đường tròn ( C là tiếp điểm ). AC cắt OM tại E, MB cắt nửa (O) tại D ( D khác B )
a. Chứng minh tứ giác ACOM nội tiếp một đường tròn
b. Chứng minh AC2=4.OE.ME
c. Chứng minh góc ADE bằng góc ACO

Giải thích các bước giải:
a,
AB là đường kính của đường tròn (O) đã cho mà C là 1 điểm nằm trên đường tròn nên:
ˆACB=90∘⇔AC⊥CB⇒AC⊥DBACB^=90∘⇔AC⊥CB⇒AC⊥DB
Vậy AC vuông góc với BD
b,
MA và MC là 2 tiếp tuyến kẻ từ M đến đường tròn nên MA=MCMA=MC hay M nằm trên trung trực của AC
OA=OC=ROA=OC=R nên O cũng nằm trên trung trực của AC
Do đó, OM là trung trực của AC hay OM⊥ACOM⊥AC mà AC⊥CBAC⊥CB nên OM//BCOM//BC
Tam giác ACD vuông tại C có AM=MC nên AM=DM
Do đó, M là trung điểm AD