cho tam giác ABC vuông cân tại A. qua điểm D thuộc cạnh BC, kẻ đường thẳng vuông góc với BC , cắt cạnh AB< AC theo thứ tự E và F. Gọi M và n theo thứ tự trung điểm của BE và CF. CMR:
a) Tứ giác AMDN là HCN?
b) AD = MN
Giúp mk với ạ : (((
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
5 tháng 8 2017
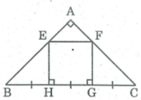
Vì ΔABC vuông cân tại A nên ∠ B = ∠ C = 45 0
Vì ΔBHE vuông tại H có ∠ B = 45 0 nên ΔBHE vuông cân tại H.
Suy ra HB = HE
Vì ΔCGF vuông tại G, có ∠ C = 45 0 nên ΔCGF vuông cân tại G
Suy ra GC = GF
Ta có: BH = HG = GC (gt)
Suy ra: HE = HG = GF
Vì EH // GF (hai đường thẳng cũng vuông góc với đường thắng thứ ba) nên tứ giác HEFG là hình bình hành (vì có một cặp cạnh đối song song bằng nhau);
Lại có ∠ (EHG) = 90 0 nên HEFG là hình chữ nhật.
Mà EH = HG (chứng minh trên).
Vậy HEFG là hình vuông.
CM
30 tháng 5 2017
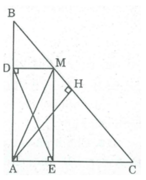
Xét tứ giác ADME, ta có:
∠ A= 90 0 (gt)
MD ⊥ AB (gt)
⇒ ∠ (ADM) = 90 0
Lại có, MD ⊥ AC ⇒ ∠ (MEA) = 90 0
Suy ra tứ giác ADME là hình chữ nhật (vì có 3 góc vuông)
∆ ABC vuông cân tại A ⇒ ∠ B = 45 0 và AB = AC = 4cm
Suy ra: ∆ DBM vuông cân tại D
⇒ DM = DB
Chu vi hình chữ nhật ADME bằng:
2(AD + DM) = 2(AD + DB) = 2AB = 2.4 = 8 (cm)
chỗ AB < AC kia các bn chuyển thành chữ " và " nhé. Mk viết nhầm