Cho đường tròn (O) đường kính AB, gọi I là trung điểm của OA. Qua điểm I vẽ dây CD vuông góc với AB, gọi K là trung điểm của BC. a) Chứng minh bốn điểm C; I; O; K cùng thuộc một đường tròn. b) Chứng minh: CI. CD = IA. IB c) Chứng minh ba điểm D, O, K thẳng hàng.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: ΔOBC cân tại O
mà OK là trung tuyến
nênOK vuông góc BC
góc CIO+góc CKO=180 độ
=>CIOK nội tiếp
b: Xét ΔICB vuông tại I và ΔIAD vuông tại I có
góc ICB=góc IAD
=>ΔICB đồng dạng với ΔIAD
=>IC/IA=IB/ID
=>IC*ID=IA*IB

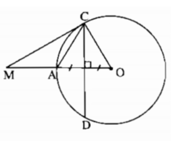
CD là đường trung trực của OA nên CA = CO.
Suy ra CA = CO = AO = AM.
Do đó ∠ (MCO) = 90 °
Vậy MC là tiếp tuyến của đường tròn (O).

a: Xét (O) có
ΔAKB nội tiếp
AB là đường kính
=>ΔAKB vuông tại K
Xét tứ giác BKHI có
góc BKH+góc BIH=180 độ
=>BKHI là tứ giác nội tiếp
b: Xét ΔAHI vuông tại I và ΔABK vuông tại K có
góc HAI chung
=>ΔAHI đồng dạng với ΔABK
=>AH/AB=AI/AK
=>AH*AK=AI*AB=1/4*R^2
