Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Bài 3:
\(AB=\sqrt{AH^2+BH^2}=\sqrt{6^2+4^2}=2\sqrt{13}\left(cm\right)\)
BC=13cm
=>\(AC=3\sqrt{13}\left(cm\right)\)
Bài 1:
a: Xét ΔBAC vuông tại A có
\(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{C}=60^0\)
Xét ΔBAC vuông tại A có
\(AB=BC\cdot\sin60^0\)
\(\Leftrightarrow BC=4\sqrt{3}\left(cm\right)\)
\(\Leftrightarrow AC=2\sqrt{3}\left(cm\right)\)
a: ΔBAC vuông tại B có góc A=45 độ
nên ΔBAC vuông cân tại B
=>BA=BC=2a
AC=căn AB^2+BC^2=2a*căn 2
b: BH=BA*BC/AC=4a^2/2*a*căn 2=a*căn 2
c: S ABC=1/2*2a*2a=2a^2
d: C=2a+2a+2a*căn 2=4a+2a*căn 2
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
Do đó: ΔABC\(\sim\)ΔHBA
b: ta có: ΔABC\(\sim\)ΔHBA
nên BA/BH=BC/BA
hay \(BA^2=BH\cdot BC\)
a.Xét tam giác ABC và tam giác HBA, có:
^B: chung
^BAC = ^BHA = 90 độ
Vậy tam giác ABC đồng dạng tam giác HBA (g.g)
b.\(\rightarrow\dfrac{AB}{HB}=\dfrac{BC}{AB}\)
\(\Leftrightarrow AB^2=BH.BC\left(đfcm\right)\) (1)
c.Áp dụng định lý pitago \(\Rightarrow BC=\sqrt{6^2+10^2}=2\sqrt{34}\left(cm\right)\)
(1) \(\Leftrightarrow6^2=2\sqrt{34}BH\)
\(\Leftrightarrow BH=\dfrac{9\sqrt{34}}{17}\left(cm\right)\)
Áp dụng định lý pitago trong tam giác ABH \(\Rightarrow AH=\sqrt{6^2-\left(\dfrac{9\sqrt{34}}{17}\right)^2}=\dfrac{15\sqrt{34}}{17}\left(cm\right)\)
Kẻ phân giác BK
Xét ΔABK vuông tại A có
\(\tan\widehat{ABK}=\dfrac{AK}{AB}\)
\(\Leftrightarrow\tan\dfrac{\widehat{ABC}}{2}=\dfrac{AK}{AB}\)(1)
Xét ΔABC có BK là đường phân giác ứng với cạnh AC(gt)
nên \(\dfrac{AK}{AB}=\dfrac{KC}{BC}\)(Tính chất đường phân giác)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AK}{AB}=\dfrac{KC}{BC}=\dfrac{AK+KC}{AB+BC}=\dfrac{AC}{AB+BC}\)(2)
Từ (1) và (2) suy ra \(\tan\dfrac{\widehat{ABC}}{2}=\dfrac{AC}{AB+BC}\)
a: Xét ΔCMD vuông tại M và ΔCAB vuông tại A có
góc C chung
=>ΔCMD đồng dạng với ΔCAB
b: Xét ΔBMI vuông tại M và ΔBAC vuông tại A có
góc MBI chung
=>ΔBMI đồng dạng với ΔBAC
=>BM/BA=BI/BC
=>BM*BC=BA*BI
c: ΔCMD đồng dạng với ΔCAB
=>CM/CA=CD/CB
=>CM/CD=CA/CB
=>ΔCMA đồng dạng với ΔCDB
=>S CMA/S CDB=(CA/CB)^2=1/4
=>S CMA=15cm2
Gọi \(I\) là giao điểm của \(AM\) và \(BN\Rightarrow IB=\dfrac{2}{3}BN;IN=\dfrac{1}{3}BN;AI=\dfrac{2}{3}AM;IM=\dfrac{1}{3}AM\)
\(\Delta ANB\) vuông tại \(A:AI^2=IB.IN\) \(\Rightarrow AI^2=\dfrac{2}{3}BN\cdot\dfrac{1}{3}BN=\dfrac{2}{9}BN^2\)
Ta cũng có trong \(\Delta ANB:AB^2=IB.BN\)
\(\Leftrightarrow a^2=\dfrac{2}{3}BN\cdot BN=\dfrac{2}{3}BN^2\Leftrightarrow BN^2=\dfrac{3}{2}a^2\)
Suy ra : \(AI^2=\dfrac{2}{9}BN^2=\dfrac{2}{9}\cdot\dfrac{3}{2}a^2=\dfrac{1}{3}a^2\).
Lại có : \(AI=\dfrac{2}{3}AM\Rightarrow AM^2=\dfrac{9}{4}AI^2=\dfrac{9}{4}\cdot\dfrac{1}{3}a^2=\dfrac{3}{4}a^2\)
\(AM\) là đường trung tuyến ứng với cạnh huyền \(BC\) của \(\Delta ABC\) vuông tại \(A\Rightarrow AM=\dfrac{1}{2}BC\Rightarrow BC^2=4AM^2=4\cdot\dfrac{3}{4}a^2=3a^2\)
\(\Rightarrow BC=\sqrt{3a^2}=a\sqrt{3}\)
\(\Delta ABC\) vuông tại \(A\) có : \(BC^2=AB^2+AC^2\left(Pythagoras\right)\)
\(\Rightarrow AC=\sqrt{BC^2-AB^2}=\sqrt{3a^2-a^2}=a\sqrt{2}\)
Vậy : \(AC=a\sqrt{2};BC=a\sqrt{3}\)
a: \(BC=\sqrt{AB^2+AC^2}=13\left(cm\right)\)
b: Xét ΔABC vuông tại A và ΔADC vuông tại A có
AC chung
AB=AD
Do đó: ΔABC=ΔADC
c: Ta có: ΔABC=ΔADC
nên BC=DC
hay ΔCBD cân tại C
a: Xét ΔABC vuông tại A và ΔADC vuông tại A có
AB=AD
AC chung
Do đó: ΔABC=ΔADC
b: Xét tứ giác BCDE có
A là trung điểm của BD
A là trung điểm của CE
Do đó: BCDE là hình bình hành
Suy ra: BC//DE
a. Pytago: \(BC=\sqrt{AB^2+AC^2}=5\left(cm\right)\)
AD là trung tuyến ứng cạnh huyền BC nên \(AD=\dfrac{1}{2}BC=2,5\left(cm\right)\)
b. Vì \(\widehat{AMD}=\widehat{AND}=\widehat{MAN}=90^0\) nên AMDN là hcn
Vậy AD=MN
c. ABC vuông cân A thì AD là trung tuyến cũng là p/g
Do đó AMDN là hình thoi(1)
Lại có D là trung điểm BC,DM//AC(⊥AB) nên M là trung điểm AB
Cmtt ta được N là trung điểm AC
Mà AB=AC nên AM=AC
Kết hợp (1) ta được AMDN là hình vuông
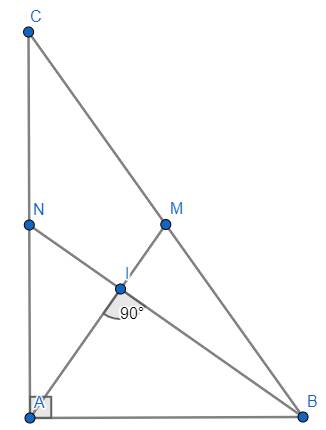
a) Xét ΔABC vuông tại A và ΔADE vuông tại A có
AC=AE(gt)
AB=AD(gt)
Do đó: ΔABC=ΔADE(hai cạnh góc vuông)
b) Ta có: ΔABC vuông tại A(gt)
⇒\(\widehat{ACB}+\widehat{B}=90^0\)(hai góc phụ nhau)(1)
Ta có: ΔAHB vuông tại H(AH⊥BC)
⇒\(\widehat{BAH}+\widehat{B}=90^0\)(hai góc phụ nhau)(2)
Từ (1) và (2) suy ra \(\widehat{ACB}=\widehat{BAH}\)
hay \(\widehat{ACH}=\widehat{BAH}\)(đpcm)
b) ΔABH vuông tai H nên
\(\widehat{B}+\widehat{BAH}+\widehat{AHB}=180^0\)
=> \(\widehat{BAH}=180^0-\widehat{B}-\widehat{AHB}=180^0-\widehat{B}-90^0\) (1)
ΔABC vuông tại A nên:
\(\widehat{B}+\widehat{BAC}+\widehat{ACB}=180^0\)
=> \(\widehat{ACB}=180^0-\widehat{B}-\widehat{BAC}=180^0-\widehat{B}-90^0\) (2)
Từ (1) và (2) => \(\widehat{BAH}=\widehat{ACB}\)