Cho tam giác đều ABC. Trên tia AB lấy điểm D sao cho B là trung điểm của AD.
a) Chứng minh tam giác BCD là tam giác cân.
b) Tính các góc của tam giác BCD.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KV
24 tháng 4 2023
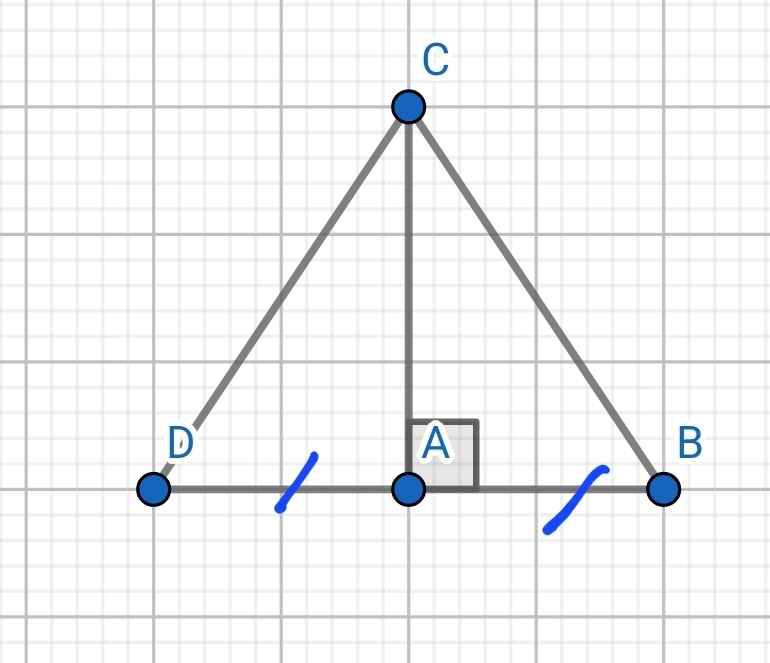
a) Xét hai tam giác vuông: ∆ABC và ∆ADC có:
AC chung
AB = AD (gt)
⇒ ∆ABC = ∆ADC (hai cạnh góc vuông)
b) Do ∆ABC = ∆ADC (cmt)
⇒ ∠BCA = ∠DCA (hai góc tương ứng)
⇒ CA là tia phân giác của ∠BCD
B
1 tháng 3 2018
b) vì tam giác ABC là tam giác đều
\(\Rightarrow\)góc DBC=60 độ.
xét tam giác BDC và tam giác ADC có:
BD=AD(GT)
[góc DBC = góc DAC=60 độ (vì tam giác ABC đều)] hoặc [DC là cạnh chung]
BC=AC(GT)
\(\Rightarrow\)tam giác BDC=tam giác ADC(c.g.c hoặc c.c.c)
\(\Rightarrow\)góc BDC=góc ADC=90 độ( vì góc BDC+ góc ADC=180 độ).
áp dụng định lí tổng 3 góc bằng 180 độ vào tam giác BDC có
góc DBC+góc BDC+góc DCB= 180 độ
\(\Rightarrow\)góc DCB= 180 độ - 60 độ - 90 độ= 30 độ.
22 tháng 12 2020
a) Xét ΔAMC và ΔDMB có
AM=DM(M là trung điểm của AD)
\(\widehat{AMC}=\widehat{DMB}\)(hai góc đối đỉnh)
MC=MB(M là trung điểm của BC)
Do đó: ΔAMC=ΔDMB(c-g-c)
⇒\(\widehat{CAM}=\widehat{BDM}\)(hai góc tương ứng)
mà \(\widehat{CAM}\) và \(\widehat{BDM}\) là hai góc ở vị trí so le trong
nên AC//BD(Dấu hiệu nhận biết hai đường thẳng song song)
b) Xét ΔAMB và ΔDMC có
AM=DM(M là trung điểm của AD)
\(\widehat{AMB}=\widehat{DMC}\)(hai góc đối đỉnh)
MB=MC(M là trung điểm của BC)
Do đó: ΔAMB=ΔDMC(c-g-c)
⇒AB=CD(Hai cạnh tương ứng)
Ta có: ΔAMC=ΔDMB(cmt)
nên AC=BD(Hai cạnh tương ứng)
Xét ΔABC và ΔDCB có
AB=DC(cmt)
AC=DB(cmt)
BC chung
Do đó: ΔABC=ΔDCB(c-c-c)
27 tháng 4 2023
a: AB<AC<BC
=>góc C<góc B<góc A
b: Xét ΔABC vuông tại A và ΔADC vuông tại A có
AB=AD
AC chung
=>ΔABC=ΔADC
=>CB=CD
=>ΔCBD cân tại C
CN
30 tháng 5 2021
a) Xét △ABC vuông tại A có :
AB2+AC2=BC2(định lý py-ta-go)
⇒ AC2=BC2-AB2
⇒ AC2=102-62
⇒ AC2=100-36
⇒ AC2=64
⇒ AC=8
Vậy AC=8cm
b)
Xét △ABC và △ADC có :
AC chung
AB=AD(gt)
∠BAC=∠DAC(=90)
⇒△ABC=△ADC(c-g-c)
⇒BC=DC(2 cạnh tương ứng)
Xét △BCD có BC=DC(cmt)
⇒△BCD cân tại C (định lý tam giác cân)
c)
Xét △BCD cân tại C có
K là trung điểm của BC (gt)
A là trung điểm của BD (gt)
⇒DK , AC là đường trung tuyến của △BCD
mà DK cắt AC tại M nên M là trọng tâm của △BCD
⇒CM=2/3AC
⇒CM=2/3.8
⇒CM=16/3cm
d)
Xét △AMQ và △CMQ có
MQ chung
MA=MC(gt)
∠AMQ=∠CMQ(=90)
⇒△AMQ=△CMQ(C-G-C)
⇒∠MAQ=∠C2(2 góc tương ứng )
QA=QC( 2 cạnh tương ứng)
Vì △ABC=△ADC(theo b)
⇒∠C1=∠C2(2 góc tương ứng)
⇒∠C1=∠MAQ
mà 2 góc này có vị trí SLT
⇒AQ//BC
⇒∠QAD=∠CBA( đồng vị )
mà∠CBA=∠CDA(△BDC cân tại C)
⇒∠QAD=∠QDA
⇒△ADQ cân tại Q
⇒QA=QD
mà QA=QC(cmt)
⇒DQ=CQ
⇒BQ là đường trung tuyến của△BCD
⇒B,M,D thẳng hàng
17 tháng 3 2023
a: AB<AC<BC
=>góc C<góc B<góc A
b: Xet ΔABC vuông tại A và ΔADC vuông tại A có
AB=AD
AC chung
=>ΔABC=ΔADC
=>CB=CD
=>ΔCBD cân tại C
c: Xet ΔCBD có
CA,BE là trung tuyến
CA căt EB tại I
=>I là trọng tâm
=>DI đi qua trung điểm của BC
a, Xét \(\Delta\) ABC có :
AB=AC
mà BD=AB
=> BCD cân tại B
b, Vì CB là đường trung tuyến của \(\Delta\) ACD
mà B là trung điểm của AD => \(\Delta\)ACD vuông tại C
Có \(\Delta\) ACB đều => ^BAC, ^ACB + ^ABC = 600
=> ^BCD = ^BDC = ^ACD-^ACB = 900- 600 =300
=> ^DBC = 1800- ^BCD- ^BDC = 1800-300-300=1200
a, Ta có :
ABC đều => AB=AC=BC
B là trung điểm của AD=> DB=BA
=> BC=BD =>Tam giác BCD cân => đpcm
b) Tính các góc của tam giác BCD
góc DBC =góc BAC+góc ACB (góc ngoài của tam giác )
ABC đều => A=B=C=60 độ
=> góc DBC =120 độ
=> góc BDC = góc BCD = \(\frac{180^0-120^0}{2}=30^0\)