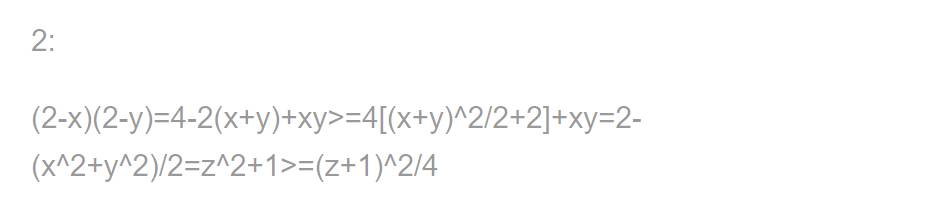Question

[Không Tên]

@Cool Kid:

\(a^3+b^3+c^3+3abc\ge\Sigma ab\sqrt{2\left(a^2+b^2\right)}\)

\(\Leftrightarrow\Sigma\frac{1}{2}\left(a+b-c\right)\left(a-b\right)^2\ge\Sigma\frac{ab\left(a-b\right)^2}{\sqrt{2\left(a^2+b^2\right)}+a+b}\)

Hay một BĐT mạnh (và đẹp:v) hơn là: 

\(\Leftrightarrow\Sigma\frac{1}{2}\left(a+b-c\right)\left(a-b\right)^2\ge\Sigma\frac{ab\left(a-b\right)^2}{2\left(a+b\right)}\)

Ta cần chứng minh: \(VT-VP=\Sigma\frac{\left(a+b-c\right)^2\left(a-b\right)^2}{2\left(a+b\right)}-\frac{\left(a-b\right)^2\left(b-c\right)^2\left(c-a\right)^2}{2\left(a+b\right)\left(b+c\right)\left(c+a\right)}\ge0\)

Giả sử \(a\ge c\ge b\) và đặt \(a=b+u+v,c=b+v\)

Bất đẳng thức này đúng theo Cauchy-Schwawrz:

\(VT-VP\ge\frac{4\left(c+a-b\right)^2\left(c-a\right)^2}{4\left(a+b+c\right)}-\frac{\left(a-b\right)^2\left(b-c\right)^2\left(c-a\right)^2}{2\left(a+b\right)\left(b+c\right)\left(c+a\right)}\ge0\)

Last inequality is: https://imgur.com/tRsHOfr (mình không gửi ảnh được nên gửi link vậy!)

Done!