từ các chữ số 0 1 2 3 4 5 có thể lập được bao nhiêu chữ số có 5 số khác nhau?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
ND
0
ND
3
CM
30 tháng 12 2017
Đáp án B
Số đó nhất thiết phải có mặt 3 chữ số 1, 2, 5 ta chỉ cần chọn 2 chữ số nữa từ 4 chữ số còn lại.
TH1: Hai chữ số được chọn kia không chứa số 0: Ta có 
TH2: Hai chữ số kia chứa chữ số 0, ta loại trường hợp chữ số 0 đứng đầu thì còn: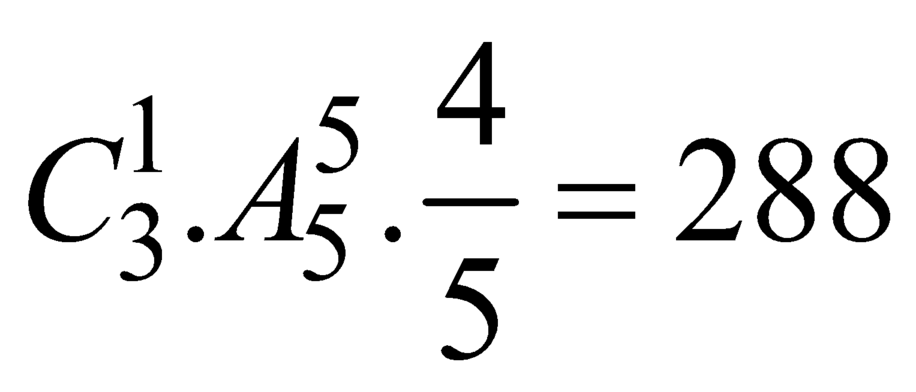 
Vậy có tất cả là 648 số
CM
5 tháng 10 2017
Gọi số cần tìm có dạng a b c d ¯ với a , b , c , d ∈ A = 0 , 1 , 2 , 3 , 4 , 5 .
Vì a b c d ¯ là số chẵn ⇒ d ∈ 0 , 2 , 4 .
TH1. Nếu d = 0 số cần tìm là a b c 0 ¯ . Khi đó: A \ 0 , a , b
a được chọn từ tập A \ 0 nên có 5 cách chọn.
b được chọn từ tập A \ 0 , a nên có 4 cách chọn.
c được chọn từ tập nên có 3 cách chọn.
Như vậy, ta có 5.4.3 = 60 số có dạng a b c 0 ¯ .
TH2. Nếu d = 2 , 4 ⇒ d : có 2 cách chọn.
Khi đó, a có 4 cách chọn (khác 0 và d), b có 4 cách chọn và c có 3 cách chọn.
Như vậy, ta có 2.4.4.3 = 96 số
Vậy có tất cả 60 + 96 = 156 số
Chọn đáp án A.
CM
1 tháng 3 2017
Gọi số cần tìm có dạng a b c d ¯ với a , b , c , d ∈ A = 0 , 1 , 2 , 3 , 4 , 5 .
Vì a b c d ¯ là số chẵn ⇒ d = 0 , 2 , 4 .
TH1. Nếu d= 0, số cần tìm là a b c 0 ¯ . Khi đó:
a được chọn từ tập A \ 0 nên có 5 cách chọn.
b được chọn từ tập A \ 0 , a nên có 4 cách chọn.
c được chọn từ tập A \ 0 , a , b nên có 3 cách chọn.
Như vậy, ta có 5.4.3 = 60 số có dạng a b c 0 ¯ .
TH2. Nếu d ∈ 2 , 4 ⇒ d có 2 cách chọn.
Khi đó, a có 4 cách chọn (khác 0 và d),
b có 4 cách chọn và c có 3 cách chọn.
Như vậy, ta có 2.4.4.3 = 96 số cần tìm như trên.
Vậy có tất cả 60 +96 = 156 số cần tìm.
Chọn đáp án A.
CM
12 tháng 9 2019
Gọi số cần tìm có dạng a b c d ¯ với a , b , c , d ∈ A = 0 , 1 , 2 , 3 , 4 , 5 .
Vì a b c d ¯ là số lẻ ⇒ d = 1 , 3 , 5 ⇒ d có 3 cách chọn.
Khi đó, a có 4 cách chọn (khác 0 và d),.
b có 4 cách chọn và c có 3 cách chọn.
Vậy có tất cả 3.4.4.3 = 144 số cần tìm.
Chọn đáp án C.
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 1 2022
a. Gọi chữ số cần lập là \(\overline{abcd}\)
TH1: \(d=0\Rightarrow\) bộ abc có \(A_9^3\) cách chọn
TH2: \(d\ne0\Rightarrow d\) có 4 cách chọn (từ 2,4,6,8)
a có 8 cách chọn (khác 0 và d), b có 8 cách chọn (khác a và d), c có 7 cách chọn (khác a,b,d)
\(\Rightarrow4.8.8.7\) số
Tổng cộng: \(A_9^3+4.8.8.7=...\)
b. Chọn 4 chữ số còn lại: có \(C_7^4\) cách
Hoán vị 3 chữ số 0,1,2: có \(3!\) cách
Coi bộ 3 chữ số này là 1 số, hoán vị với 4 chữ số còn lại: \(5!\) cách
Ta đi tính số trường hợp 0 đứng đầu:
Số 0 đứng đầu trong bộ 0,1,2: có \(2!\) cách
Đặt bộ 0,1,2 đứng đầu, xếp vị trí cho 4 chữ số còn lại: \(4!\) cách
Vậy có: \(C_7^4.\left(3!.5!-2!.4!\right)=...\) số
Có 5 cách chọn hàng chục nghìn
Có 5 cách chọn hàng nghìn
Có 4 cách chọn hàng trăm
Có 3 cách chọn hàng chục
Có 2 cách chon hàng đơn vị
Suy ra có tất cả 5 x 5 x 4 x 3 x 2 = 600 số