Cho hình bình hành ABCD. Gọi H, K lần lượt là trung điểm của AB và CD.
1) Chứng minh AHKD là hình bình hành.
2) Gọi I là giao điểm của AK và DH; J là giao điểm của HC và KB. Chứng minh IJ//CD
v à I J 12 C D .
3) Chứng minh ba đường thẳng IJ, AC, HK đồng quy.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 11 2021
a: Xét tứ giác BMDN có
BM//DN
BM=DN
Do đó: BMDN là hình bình hành
31 tháng 10 2021
a: Xét tứ giác BMDN có
BM//DN
BM=DN
Do đó: BMDN là hình bình hành
16 tháng 12 2020
a) Ta có: \(AE=EB=\dfrac{AB}{2}\)(E là trung điểm của AB)
\(CF=FD=\dfrac{CD}{2}\)(F là trung điểm của CD)
mà AB=CD(Hai cạnh đối của hình bình hành ABCD)
nên AE=CF=FD=EB
Xét tứ giác AECF có
AE//CF(AB//CD, E∈AB, F∈CD)
AE=CF(cmt)
Do đó: AECF là hình bình hành(Dấu hiệu nhận biết hình bình hành)
b) Xét tứ giác AEFD có
AE//FD(AB//CD, E∈AB, F∈CD)
AE=FD(cmt)
Do đó: AEFD là hình bình hành(Dấu hiệu nhận biết hình bình hành)
c) Ta có: AF//CE(Hai cạnh đối trong hình bình hành AECF)
mà H∈AF(gt)
và K∈CE(gt)
nên HF//KC và EK//AH
Xét ΔDKC có
F là trung điểm của CD(gt)
FH//DK(cmt)
Do đó: H là trung điểm của DK(Định lí 1 về đường trung bình của tam giác)
⇒DH=KH(1)
Xét ΔABH có
E là trung điểm của AB(gt)
EK//BH(cmt)
Do đó: K là trung điểm của BH(Định lí 1 về đường trung bình của tam giác)
⇒BK=KH(2)
Từ (1) và (2) suy ra DH=HK=KB(đpcm)
21 tháng 9 2021
a: Xét tứ giác DMBN có
BM//DN
BM=DN
Do đó: DMBN là hình bình hành
b: Xét ΔAKB có
M là trung điểm của AB
MH//BK
Do đó: H là trung điểm của AK
Xét ΔCHD có
N là trung điểm của CD
NK//DH
Do đó: K là trung điểm của HC
CM
17 tháng 10 2018
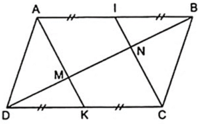
Áp dụng định nghĩa, tính chất và theo giả thiết của hình bình hành, ta có:
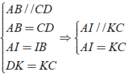
Tứ giác AICK có cặp cạnh đối song song và bằng nhau nên AICK là hình bình hành.
