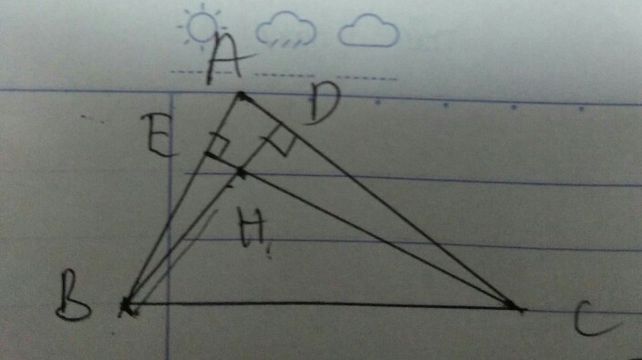
Cho tam giác nhọn ABC có AB<AC và trực tâm là T. Gọi H là chân đường cao kẻ từ A của tam giác ABC và D là điểm đối xứng với T qua đường thẳng BC; I và K lần lượt là hình chiếu vuông góc của D trên AB và AC; E và F lần lượt là trung điểm của AC và IH
a) Chứng minh ABDC là tứ giác nội tiếp và tam giác ACD và IHD đồng dạng
b) Chứng minh I,H,K thẳng hàng và DÈ là tam giác vuông
c) Chứng minh \(\frac{BC}{DH}=\frac{AB}{DI}+\frac{AC}{DK}\)