Cho tam giác ABC ( AB =AC ). trên tia BA lấy điểm D sao cho A là trung điểm của BD
a) Chứng minh góc BCD = góc ABC + góc ADC
b) Chứng minh góc BCD = 90 độ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KV
24 tháng 4 2023
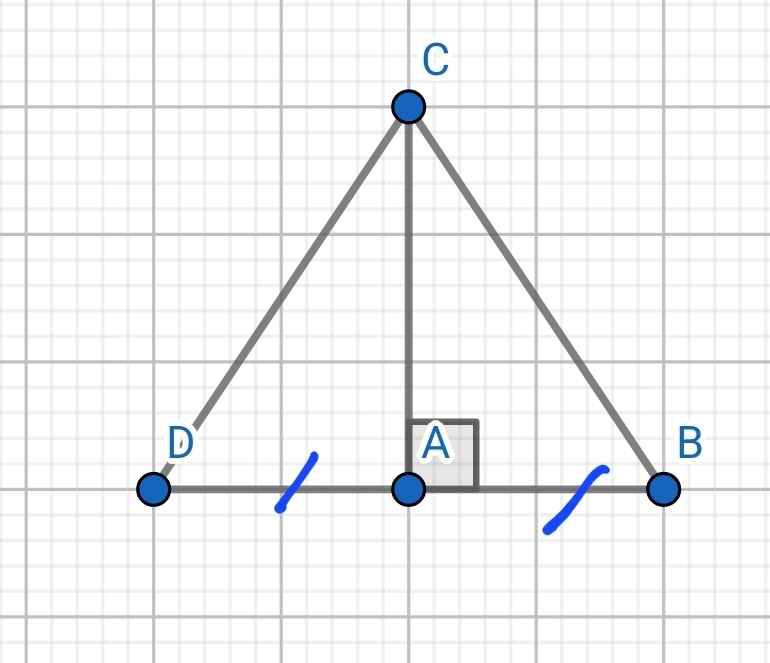
a) Xét hai tam giác vuông: ∆ABC và ∆ADC có:
AC chung
AB = AD (gt)
⇒ ∆ABC = ∆ADC (hai cạnh góc vuông)
b) Do ∆ABC = ∆ADC (cmt)
⇒ ∠BCA = ∠DCA (hai góc tương ứng)
⇒ CA là tia phân giác của ∠BCD
22 tháng 12 2021
a: Xét ΔACI và ΔMCI có
CA=CM
ˆACI=ˆMCIACI^=MCI^
Do đó: ΔACI=ΔMC
12 tháng 12 2021
a: Xét ΔCIA và ΔDIB có
IC=ID
\(\widehat{CIA}=\widehat{DIB}\)
IA=IB
Do đó: ΔCIA=ΔDIB
Xét tam giác ABC ,có:
AB=AC
=> tam giác ABC cân tại A
=> góc ABC = góc ACB
vì A là trung điểm của BD (gt)
=> AB = AD
Mà AB = AC ( gt)
=> AD = AC
=> tam giác ACD là tam giác cân tại A
=> góc ACD = góc ADC
có góc BCD = góc ACB + góc ACD ( hệ thức cộng góc )
mà góc ABC = góc ACB(cmt) ; góc ADC = góc ACD (cmt)
=> góc BCD = góc ABC + góc ADC
=> đpcm
còn câu b mk chx nghĩ ra =.=///
hok tốt
Nguyễn Ngọc Linh làm câu a rùi nha. mk làm câu b cho
Ta có A là trung điểm của BD
=> AB=1/2.BD
Mà theo bài ra AB=AC
=>AC=1/2.BD
Xét tam giác BCD có : AC là đường trung tuyến bằng 1/2 cạnh đối diện
=> tam giác BCD vuông tại C
=> góc BCD= 90 độ