cho tam giac abc trên cạnh BC lấy điểm D nằm giữa hai điểm B và C Qua D vẽ đường thẳng song song với AB cắt AC tại E và đường thẳng song song với AC cát AB tại F gọ H là chân đường cao kẻ từ A đến BC O là giao điểm của AD và EF Chứng minh tam giác AOH cân ? điểm D nằm ở đâu trên cạnh BC để độ dài FE là nhỏ nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BF
25 tháng 2 2023
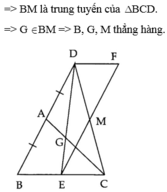
Tứ giác `DACM` có:
`DA` // `MC`
`DM` // `AC`
`=>` Tứ giác `DACM` là hình bình hành
`=> hat{D} = hat{C}; DA = MC`
Tương tự:
Tứ giác `AEMB` là hình bình hành có `hat{B} = hat{E}; AE = BM`
Ta có:
* `DE = DA + AE`
* `BC = BM + MC`
mà `DA = MC; AE = BM`
`=> DE = MC`
Xét tam giác `MDE` và tam giác `ACB` có:
`hat{B} = hat{E}`
` DE = MC`
`hat{D} = hat{C}`
`=>` tam giác `MDE =` tam giác `ACB` (góc - cạnh - góc)
CM
19 tháng 4 2017
Ta chứng minh được AEDF là hình bình hành Þ AD Ç È = I. I là trung điểm của AD và EF. Suy ra E đối xứng với F qua I
15 tháng 1 2022
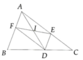
a. Xét tam giác ABC có:
DE//BC (gt)
=>\(\dfrac{DA}{DB}=\dfrac{EA}{EC}\)(định lý Ta-let) (1)
Xét tam giác ADE có:
AD//CF (gt)
=>\(\dfrac{EA}{EC}=\dfrac{DE}{EF}\)(định lý Ta-let) (2)
Từ (1) và (2) suy ra:\(\dfrac{DA}{DB}=\dfrac{ED}{FE}\)
H
30 tháng 11 2014
D là TĐ của AB mà DE //BC nên DE là đg TB của tam giác ABC -->E là TĐ của AC.
E là TĐ của AC mà EF //AB nên EF là đg TB của tam giác CAB--->F là TĐ của BC
BÀI NÀY MÌNH KO CHÈN ĐƯỢC HÌNH MONG BẠN THÔNG CẢM !!!
a. Xét tứ giác AEDF có: AF // DE
AE // DF
\(\Rightarrow\) AEDF là hình bình hành
\(\Rightarrow\)AD cắt EF tại trung điểm mỗi đường.
Mà O là giao của AD và EF
\(\Rightarrow\) O là trung điểm AD
Mà \(\Delta AHD\) vuông tại H
\(\Rightarrow\) HO = AO
Do đó \(\Delta AOH\) cân tại O