Cho hình vuông abcd .Trên tia đối của ba lấy e trên tia đối của cb lấy f sao cho ae= cf các điểm k,h thứ tự đi chuyển trên ab,ad sao cho bk=ah xác định vị trí h k sao cho hk có độ dài nhỏ nhất
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


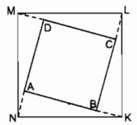
Xét △ ANK và △ BKL :
AN = BK (gt)
∠ A = ∠ B = 90 0
AK = BL (vì AB = BC, BK = CL)
Do đó △ ANK = △ BKL (c.g.c)
⇒ NK = KL (1)
Xét △ BKL và △ CLM:
BK = CL (gt)
∠ B = ∠ C = 90 0
BL = CM (vì BC = CD, CL = DM)
Do đó: △ BKL = △ CLM (c.g.c)
⇒ KL = LM (2)
Xét △ CLM và △ DMN :
CL = DM (gt)
∠ C = ∠ D = 90 0
CM = DN (vì CD = DA, DM = AN)
Do đó: △ CLM = △ DMN (c.g.c)
⇒ LM = MN (3)
Từ (1), (2) và (3) ⇒ NK = KL = LM = MN
Tứ giác MNKL là hình thoi
△ ANK = △ BKL ⇒ ∠ (ANK) = ∠ (BKL)
Trong tam giác ANK có A là góc vuông ⇒ ∠ (ANK) + ∠ (AKN) = 90 0
⇒ ∠ (BKL) + ∠ (AKN) = 90 0 hay ∠ (NKL) = 90 0
Vậy tứ giác MNKL là hình vuông.

Bài 2:
a: Ta có: ΔABD cân tại B
mà BH là đường cao
nên H là trung điểm của AD
hay AH=DH

Bạn tự vẽ hình nhé. Nếu cần hình thì ib mình.
Xét ΔADE và ΔABC có:
AD = AB (gt)
\(\widehat{DAE}=\widehat{BAC}\)(đối đỉnh)
AE = AC (gt)
=> ΔADE = ΔABC (c.g.c)
=> \(\widehat{EDA}=\widehat{ABC}\)(2 góc tương ứng)
=> ED//BC (1)
Xét ΔAKD và ΔADH có:
AD = AB (gt)
\(\widehat{EDA}=\widehat{ABC}\)(cmt)
BH = DK (gt)
=> ΔAKD = ΔABH (c.g.c)
=> \(\widehat{AKD}=\widehat{ABH}=90^o\)
=> \(AK\perp ED\)(2)
từ (1) và (2) => \(AK\perp BC\)
mà \(AH\perp BC\)
=> đpcm
Học tốt ^^
