Cho hai lực F1 và F2 có độ lớn F1=F2=6N. Vẽ hợp lực và tìm độ lớn của hợp lực khi
1. F1 cùng chiều F2
2. Góc ( F1,F2 ) = 120°
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
20 tháng 11 2018
Chọn đáp án C
Hai lực thành phần F1 = F2 hợp nhau bất kỳ thì hợp lực:
HT
16 tháng 10 2019
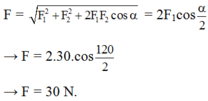
Áp dụng công thức: \(F^2=F_1^2+F_2^2+2.F_1.F_2.\cos\left(\widehat{F_1;F_2}\right)\)
a/ \(\overrightarrow{F_1}\uparrow\uparrow\overrightarrow{F_2}\Rightarrow\left(\widehat{F_1;F_2}\right)=0\Rightarrow\cos0=0\)
Thay số vào tìm đc F
b/ \(\overrightarrow{F_1}\uparrow\downarrow\overrightarrow{F_2}\Rightarrow\left(\widehat{F_1;F_2}\right)=180^0\Rightarrow\cos\left(\widehat{F_1;F_2}\right)=-1\)
Thay vào
c/ \(\left(\widehat{F_1;F_2}\right)=90^0\Rightarrow\cos90^0=0\)
d/ làm tương tự
VT
18 tháng 5 2019
Chọn đáp án C
? Lời giải:
+ Các lực được biểu diễn như hình vẽ
VT
21 tháng 3 2017
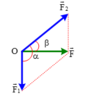
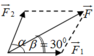
Vì F 1 = F 2 mà F 1 → ; F 2 → tạo thành hình bình hành với đường chéo là F → nên α = 2 β = 2.30 0 = 60 0
Ta có F = 2. F 1 cos α 2
⇒ F = 2.50. 3 . cos 30 0 = 100. 3 . 3 2 = 150 N
1/ Khi \(\overrightarrow{F_1}\uparrow\uparrow\overrightarrow{F_2}\Rightarrow\cos\left(\widehat{F_1;F_2}\right)=\cos0=0\)
\(\Rightarrow F^2=F_1^2+F_2^2\Leftrightarrow F=\sqrt{6^2+6^2}=6\sqrt{2}\left(N\right)\)
2/ \(F^2=F_1^2+F_2^2+2.F_1.F_2.\cos\left(\widehat{F_1;F_2}\right)\)
\(F=\sqrt{6^2+6^2+2.6.6.\cos120}=6\left(N\right)\)