Cho ABC nội tiếp (O) và trực tâm H. Kẻ đường kính AD a) Chứng minh rằng BHCD là hình hành b) Gọi E là điểm đối xứng của H qua O. Chứng minh rằng vecto HA + HB + HC = Vecto HE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 8 2022
Câu 1:
Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó MN là đường trung bình
=>MN//BC và MN=BC/2(1)
Xét ΔHBC có
E là trung điểm của HB
F là trung điểm của HC
Do đó: EF là đường trung bình
=>EF//BC và EF=BC/2(2)
Từ (1) và (2) suy ra MN//EF và MN=EF
=>MNFE là hình bình hành
SUy ra: VECTO MN=VECTO EF
CM
27 tháng 3 2018
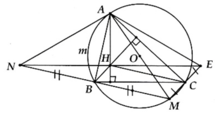
a, BH ^ AC và CM ^ AC Þ BH//CM
Tương tự => CH//BM
=> BHCM là hình bình hành
b, Chứng minh BNHC là hình bình hành
=> NH//BC
=> AH ^ NH => A H M ^ = 90 0
Mà A B N ^ = 90 0 => Tứ giác AHBN nội tiếp
c, Tương tự ý b, ta có: BHEC là hình bình hành. Vậy NH và HE//BC => N, H, E thẳng hàng
d, A B N ^ = 90 0 => AN là đường kính đường tròn ngoại tiếp tứ giác AHBN
AN = AM = 2R, AB = R 3 => A m B ⏜ = 120 0
S A O B = 1 2 S A B M = R 2 3 4
S A m B ⏜ = S a t A O B - S A O B = R 2 12 4 π - 3 3
=> S cần tìm = 2 S A m B ⏜ = R 2 6 4 π - 3 3
CM
25 tháng 2 2018
a, Ta có: BD//CH vì cùng vuông góc với AB; BH//CD vì cùng vuông góc với AC
b, Ta có I là trung điểm của BC => I là trung điểm HD
c, Ta có OI là đường trung bình ∆AHD => AH = 2OI
6 tháng 1 2022
1: Xét tứ giác BHCD có
O là trung điểm của BC
O là trung điểm của HD
Do đó: BHCD là hình bình hành
Gọi BE, CF, AN là đường cao của TAM GIÁC ABC
Vì BE//DC⇒BH//DC(1)
CF//BD⇒CD//BH(2)
Từ (1)và(2)⇒BHCD là hình bình hành