Cho tam giác nhọn ABC nội tiếp đường tròn tâm O. Gọi H là trực tâm của tam giác ABC. Gọi M,N lần lượt là trung điểm của BC và AH. Chứng minh: vecto OM = vecto AN
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
27 tháng 9 2019
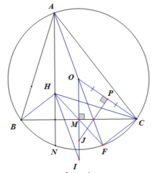
a) Gọi F là điểm đối xứng với A qua O ⇒ AF là đường kính của (O)
Ta có ACF = ABF = 90o (góc nội tiếp chắn nửa đường tròn) ⇒ AC ⊥ CF , AB ⊥ BF
Mà BH ⊥ AC, CH ⊥ AB ⇒ CF // BH, BF // HC
Suy ra BHCF là hình bình hành ⇒ Trung điểm M của BC cũng là trung điểm của HF.
⇒ OM là đường trung bình của ∆ AHF ⇒ AH = 2OM
13 tháng 6 2023
a: góc AMO=góc AFO=góc ANO=90 độ
=>A,M,F,O,N cùng thuộc 1 đường tròn
b: Gọi I là giao của MN với AO
=>I là trung điểm của MN
AI*AO=AM^2
Xét ΔAMH và ΔAFM có
góc AMH=góc AFM
góc MAH chung
=>ΔAMH đồng dạng với ΔAFM
=>AH*AF=AI*AO
=>góc AHI=góc AOF
=>OFHI nội tiếp
=>M,N,H thẳng hàng
5 tháng 7 2021
a) Xét tứ giác OCDB có
\(\widehat{OBD}+\widehat{OBC}=180^0\)
Do đó: OCDB là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
CM
21 tháng 6 2017
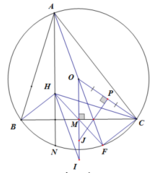
b) Vì AHIO là hình bình hành nên OI = AH = 2OM
Gọi P là trung điểm OC ⇒ PJ là trung trực OC ⇒ PJ ⊥ OC.
Có OM là trung trực BC ⇒ OM ⊥ BC. Suy ra
Δ O J P ~ Δ O C M ( g . g ) ⇒ O J O C = O P O M ⇒ O J . O M = O C . O P ⇒ O J .2 O M = O C .2 O P ⇒ O J . O I = O C . O C = R 2
