tính độ dài các cạnh của 1 tam giác biết chu vi tam giác đó bằng 45cm và độ dài các cạnh tỉ lệ với 2;3;4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HB
26 tháng 12 2017
gọi các cạnh cú tam giác đó là a;b;c (>o)(cm)
theo bài ra ta có
a/3=b/5=c/7 và a+b+c=45
áp dụng.....ta có
a/3=b/5=c/7=a+b+c/3+5+7=45/15=3
a/3=3 thì a=9
b/5=3 thì b=15
c/7=3 thì c=21
9 tháng 1 2023
a: Gọi độ dài ba cạnh lần lượt là a,b,c
Theo đề, ta có: a/4=b/5=c/7 và a+b+c-2a=2
Áp dụng tính chất của DTBSN, ta được:
\(\dfrac{a}{4}=\dfrac{b}{5}=\dfrac{c}{7}=\dfrac{a+b+c-2a}{4+5+7-2\cdot4}=\dfrac{2}{8}=\dfrac{1}{4}\)
=>a=1; b=5/4; c=7/4
b: Gọi độ dài ba cạnh lần lượt là a,b,c
Theo đề, ta có:
a/2=b/4=c/5
Áp dụng tính chất của DTSBN, ta đc:
\(\dfrac{a}{2}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b+c}{2+4+5}=\dfrac{33}{11}=3\)
=>a=6; b=12; c=15
14 tháng 10 2019
a, Gọi độ dài các cạnh của tam giác đó là a,b,c ( a,b,c thuộc N*,cm)
Theo đề ra: \(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}\) và a+b+c=45 (cm)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}=\frac{a+b+c}{3+5+7}=\frac{45}{15}=3\)
\(\frac{a}{3}=3\Rightarrow a=9\)
\(\frac{b}{5}=3\Rightarrow b=15\)
\(\frac{c}{7}=3\Rightarrow c=21\)
Vậy độ dài các cạnh của tam giác đó là: 9cm, 15cm,21cm
b,Gọi độ dài các cạnh của tam giác đó là a,b,c ( a,b,c thuộc N*,cm)
cạnh lớn nhất là c, cạnh nhỏ nhất là a
Theo đề ra: \(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}\)và \(c+a-b=20\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}=\frac{c+a-b}{7+3-5}=\frac{20}{5}=4\)
\(\frac{a}{3}=4\Rightarrow a=12\)
\(\frac{b}{5}=4\Rightarrow b=20\)
\(\frac{c}{7}=4\Rightarrow c=28\)
Vậy độ dài các cạnh của tam giác đó là: 12cm,20cm,28cm
26 tháng 12 2021
Gọi 3 cạnh của tam giác lần lượt là a, b, c
Theo đề, ta có: \(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}\)và a + b + c = 36
Theo tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{3+4+5}=\frac{36}{12}=3\)
=> a = 3.3 = 9; b = 3.4 = 12; c = 3.5 = 15
Vậy độ dài 3 cạnh của tam giác đó lần lượt là 9cm, 12cm, 15cm.
CM
22 tháng 5 2017
Gọi độ dài các cạnh của tam giác lần lượt là x, y, z (cm)
Theo đề bài ta có x + y + z = 36 và
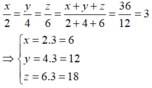
Chọn đáp án B
26 tháng 10 2016
gọi :ba cạnh của hình tam giác là a ,b,c
ta có :\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}=\frac{a+b+c}{3+5+7}=\frac{40,5}{15}=2,7\)
áp dụng tính chất dãy tỉ số bằng nhau :
\(\frac{a}{3}=2,7\Rightarrow a=2,7.3=8,1\)
\(\frac{b}{5}=2,7\Rightarrow b=2,7.5=13,5\)
\(\frac{c}{7}=2,7\Rightarrow c=2,7.7=18,9\)
đáp số : 3 cạnh hình vuông có chiều dài là :18,9;13,5;8,1
26 tháng 10 2016
Gọi độ dài 3 cạnh của 1 tam giác lần lượt là a, b, c (cm)
Theo đề bài ta có:
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}\)
\(a+b+c=40,5\)
Áp dụng tính chất của dãy tỉ số bằng nhau
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}=\frac{a+b+c}{3+5+7}=\frac{40,5}{15}=2,7\)
\(\cdot\frac{a}{3}=2,7\Rightarrow a=2,7.3=8,1\)
\(\cdot\frac{b}{5}=2,7\Rightarrow b=2,7.5=13,5\)
\(\cdot\frac{c}{7}=2,7\Rightarrow c=2,7.7=18,9\)
Vậy độ dài 3 cạnh của 1 tam giác lần lượt là 8,1cm; 13,5cm; 18,9cm
28 tháng 11 2021
\(a,\) Gọi độ dài 3 cạnh là a,b,c(cm;0<a<b<c<120)
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b+c}{3+4+5}=\dfrac{120}{12}=10\\ \Rightarrow \begin{cases} a=10.3=30\\ b=10.4=40\\ c=10.5=50 \end{cases} \)
Vậy ...
\(b,\) Gọi độ dài 3 cạnh là a,b,c(cm;0<a<b<c)
\(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{7}=\dfrac{c-a}{7-3}=\dfrac{80}{4}=20\\ \Rightarrow \begin{cases} a=20.3=60\\ b=20.5=100\\ c=20.7=140 \end{cases}\\ \Rightarrow P=a+b+c=300(cm)\)
29 tháng 10 2021
gọi x,y,z (cm) là độ dài lần lượt 3 cạnh của tam giác (x,y,z ∈ N*)
Nửa chu vi của hình tam giác đó là: 126:2= 63
Theo đề bài, ta có: \(\dfrac{x}{2}\)=\(\dfrac{y}{3}\)=\(\dfrac{z}{4}\)và x+y+z = 63
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{2}\)=\(\dfrac{y}{3}\)=\(\dfrac{z}{4}=\dfrac{x+y+z}{2+3+4}=\dfrac{63}{9}=7\)
vì \(\dfrac{x}{2}=9\Rightarrow x=9.2=18\)
\(\dfrac{y}{3}=9\Rightarrow y=9.3=27\)
\(\dfrac{z}{4}=9\Rightarrow z=9.4=36\)
Vậy x = 18; y= 27; z= 36
Dễ v:, làm chơi
Gọi ba cạnh của tam giác là a,b,c (cm)
Theo đề, ta có: \(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}=\frac{a+b+c}{2+3+4}=\frac{45}{9}=5\)
\(\Rightarrow\hept{\begin{cases}a=5.2=10\\b=5.3=15\\c=5.4=20\end{cases}}\)
gọi tam giác đó là x; y; z, ta có:
các cạnh x; y; z tỉ lệ với các số 2; 3; 4, ta có:
\(\frac{x}{2}=\frac{y}{3}=\frac{z}{4}\)
ap dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{x}{2}=\frac{y}{3}=\frac{z}{4}=\frac{x+y+z}{2+3+4}=\frac{45}{9}=5\)
=> x = 5.2 = 10 (cm)
y = 5.3 = 15 (cm)
z = 5.4 = 20 (cm)
vậy: độ dài các cạnh lần lượt là: 10; 15; 20