Cho đường tròn tâm O, đường kính AD= 2R. Vẽ cung tròn tâm D, bán kinh R. Cung này cắt đường tròn O tại B và C.
a) OBDC là hình gì? Vì sao?
b) Tính \(\widehat{CDB},\widehat{CBO},\widehat{OBA}\)
c) Chứng minh \(\Delta ABC\)đều
Thanks
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

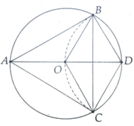
a, HS Tự chứng minh
b, Tính được C B D ^ = C B O ^ = O B A ^ = 30 0
c, Chứng minh ∆ABC cân tại A có: A B C ^ = 60 0 => ∆ABC đều

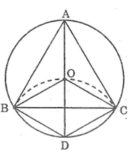
Ta có:
OB = OC = R (vì B, C nằm trên (O; R))
DB = DC = R (vì B, C nằm trên (D; R))
Suy ra: OB = OC = DB = DC
Vậy tứ giác OBDC là hình thoi
a) Ta có:
OB = OC = R (vì B, C nằm trên (O ; R))
DB = DC = R ( vì B, C nằm trên (D ; R))
Suy ra : OB = OC = DB = DC.
Vậy tứ giác OBDC là hình thoi.
b) Ta có: OB = OD = BD = R
∆OBD đều ⇒ˆOBD=60∘
Vì OBDC là hình thoi nên:
ˆCBD=ˆOBC=12ˆOBD=30∘CBD^=OBC^=12OBD^=30∘
Tam giác ABD nội tiếp trong (O) có AD là đường kính nên:
ˆABD=90∘ABD^=90∘
Mà ˆOBD+ˆOBA=90∘OBD^+OBA^=90∘
Nên ˆOBA=ˆABD–ˆOBD=90∘–60∘=30∘OBA^=ABD^–OBD^=90∘–60∘=30∘
c) Tứ giác OBDC là hình thoi nên OD ⊥ BC hay AD ⊥ BC
Ta có: AB = AC ( tính chất đường trung trực)
Suy ra tam giác ABC cân tại A (1)
Mà ˆABC=ˆOBC–ˆOBA=30∘+30∘=60∘ABC^=OBC^–OBA^=30∘+30∘=60∘. (2)
Từ (1) và (2) suy ra tam giác ABC đều.