mong mn giúp em với ạ em cần gấp em xin cảm ơn ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LC
1
5 tháng 8 2021
37
ta thấy khi cân bằng nhiệt mực nước giảm 0,5cm chứng tỏ đá tan
\(=>\Delta h=0,45-0,25=0,2m\)
\(=>Dđ.V2=Dn.V1=>900.S.h=Dn.S\left(h-0,005\right)\)
\(=>h=0,05m< 0,25m\)=>đá chưa tan hết\(=>tcb=0^oC\)
\(=>Qtoa=Dn.S.\Delta h.t1.4200=1000.S.0,2.t1.4200=840000St1\left(J\right)\)
\(=>Qthu1=0,25.S.Dđ.2100.20=9450000S\left(J\right)\)
\(=>Qthu2=S.0,05.900.340000=15300000S\left(J\right)\)
\(=>840000St1=24750000S=>t1=29,5^oC\)
LC
3
Q
3 tháng 8 2021
a, khi cân bằng nhiệt ta có \(0,5.3,4.10^5+0,5.\left(4200+2100+400\right).t=1.\left(50-t\right).4200\Rightarrow t=5,3^oC\)
b, để nhiệt cân bằng hệ bằng 0 thì lượng nước đá p tan vừa đủ
\(m_đ.3,4.10^5=1.50.4200\Rightarrow m_đ\approx0,617\left(kg\right)\)
1N
0
MR
1
V
0
NL
3
20 tháng 10 2021
a) ĐKXĐ: \(\left\{{}\begin{matrix}x\le-1\\x\ge2\end{matrix}\right.\)
\(\sqrt{x^2-x-2}-\sqrt{x-2}=0\\ \Leftrightarrow\sqrt{x^2-x-2}=\sqrt{x-2}\\ \Leftrightarrow x^2-x-2=x-2\\ \Leftrightarrow x^2-2x=0\\ \Leftrightarrow x\left(x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\left(ktm\right)\\x=2\left(tm\right)\end{matrix}\right.\)
20 tháng 10 2021
\(a,ĐK:x\ge2\\ PT\Leftrightarrow x^2-x-2=x-2\\ \Leftrightarrow x^2-2x=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\x=0\left(ktm\right)\end{matrix}\right.\Leftrightarrow x=2\\ b,ĐK:\left[{}\begin{matrix}x\le-1\\x\ge1\end{matrix}\right.\\ PT\Leftrightarrow\sqrt{x^2-1}=x^2-1\\ \Leftrightarrow x^2-1=\left(x^2-1\right)^2\\ \Leftrightarrow\left(x^2-1\right)\left(x^2-1-1\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x+1\right)\left(x-\sqrt{2}\right)\left(x+\sqrt{2}\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\left(tm\right)\\x=-1\left(tm\right)\\x=\sqrt{2}\left(tm\right)\\x=-\sqrt{2}\left(tm\right)\end{matrix}\right.\)
\(c,ĐK:\left[{}\begin{matrix}x\le-2\\x\ge1\end{matrix}\right.\\ PT\Leftrightarrow\sqrt{x^2-x}=-\sqrt{x^2+x-2}\\ \Leftrightarrow x^2-x=x^2+x-2\\ \Leftrightarrow2x=2\\ \Leftrightarrow x=1\left(tm\right)\)
V
1
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 9 2021
ĐKXĐ: \(x\ge1\)
\(\sqrt{x-1-4\sqrt{x-1}+4}+\sqrt{x-1-6\sqrt{x-1}+9}=0\)
\(\Leftrightarrow\sqrt{\left(\sqrt{x-1}-2\right)^2}+\sqrt{\left(3-\sqrt{x-1}\right)^2}=0\)
\(\Leftrightarrow\left|\sqrt{x-1}-2\right|+\left|3-\sqrt{x-1}\right|=0\)
Do \(\left|\sqrt{x-1}-2\right|+\left|3-\sqrt{x-1}\right|\ge\left|\sqrt{x-1}-2+3-\sqrt{x-1}\right|=1>0\) với mọi x thuộc TXĐ
\(\Rightarrow\) Phương trình đã cho vô nghiệm
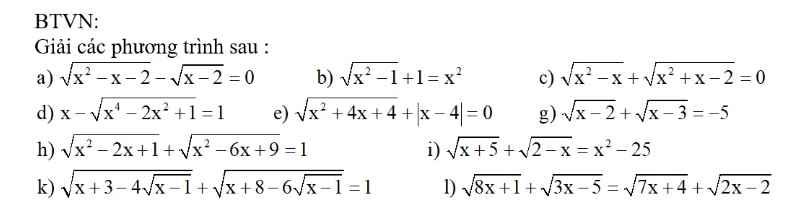
câu hỏi đâu bạn
dạ nãy em đăng bị lỗi em mới đăng lại rồi ạ