Cho tam giác ABC có ba góc nhọn, hai đường cao BE và CF cắt nhau tại H.
a) Chứng minh tam giác BHF đồng dạng vs tam giác CHE
b) Chứng minh AF.AB = AE.AC
c) Chứng minh tam giác AEF đồng dạng tam giác ABC
d) Kẻ AH cắt BC tại I.
Chứng minh EB là tia phân giác của góc FEI






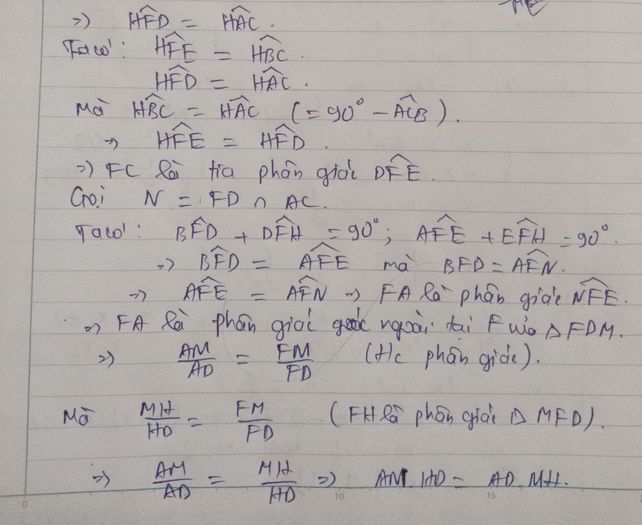 Bạn tham khảo cách làm nhé!
Bạn tham khảo cách làm nhé!
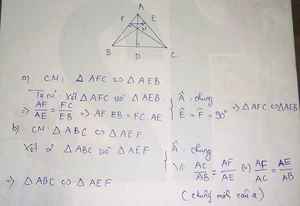




Giải
a) Xét \(\Delta BHF\) và \(\Delta CHE\) có:
\(\widehat{BHF}=\widehat{CHE}\) (vì đối đỉnh)
\(\widehat{BFH}=\widehat{CEH}=90^o\)
=> \(\Delta BHF\) \(\Delta CHE\) (g - g)
b) Xét \(\Delta ABE\) và \(\Delta ACF\) có:
\(\widehat{A}\) là góc chung
\(\widehat{AEB}=\widehat{AFC}=90^o\)
=> \(\Delta ABE\) \(\Delta ACF\) (g - g)
=> \(\frac{AB}{AC}=\frac{AE}{AF}\)
=> AF . AB = AE . AC
c) Xét \(\Delta AEF\) và \(\Delta ABC\) có:
\(\widehat{A}\) là góc chung
\(\frac{AE}{AB}=\frac{AF}{AC}\) (vì \(\Delta ABE\) \(\Delta ACF\))
=> \(\Delta AEF\) \(\Delta ABC\) (c - g - c)
d) Câu d mình không nghĩ ra. Bạn tự làm nha, chắc là xét tam giác đồng dạng rồi suy ra hai góc bằng nhau và sẽ suy ra đường phân giác đó.