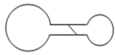
Hai bình V1,V2=2V1 được nối với nhau bằng 1 ống nhỏ cách nhiệt hai bình chứa oxi ở áp suất Po=105N/cm3 và ở nhiệt độ t0=3000K.sau đó người ta cho bình V1 giảm nhiệt đến t1=2500K. bình V2 tăng nhiệt đến t2=3500K. tính áp suất khí lúc này ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
17 tháng 6 2017
Chọn D.
Khóa mở: p1 = pm = 105 Pa
Đối với bình 1 quá trình diễn ra trước khi K mở là quá trình đẳng tích.
Chênh lệch áp suất hai bên sau khi K mở: ∆p = 105 Pa
Bình 1 ban đầu: p0.V1 = ν.R.T0
Sau khi khóa K mở: (p + ∆p).V1 = ν1.R.T
Ở bình 2 sau khi K mở ta có: p.V2 = ν2.R.T
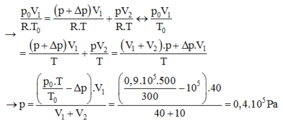
Mặt khác: ν = ν1 + ν2
VT
17 tháng 11 2018
Chọn D.
Tới nhiệt độ nào thì van mở:
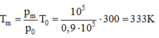
Bắt đầu từ nhiệt độ Tm áp suất trong bình 1 tăng nhanh hơn trong bình 2, nhưng khi hiệu áp suất vượt quá 105 Pa thì van lại mở. Van giữ cho hiệu áp suất là 105 Pa trong quá trình tăng nhiệt độ cho đến khi T = 500 K. Khi đó:
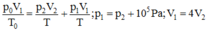
Ta có p1 = 1,4.105 Pa , từ đó rút ra p2 = 0,4.105 Pa
VT
20 tháng 3 2019
Khi khóa K mở (bình đã thông nhau). Gọi p 1 ' và p 2 ' là áp suất riêng phần của chất khí thứ nhất và thứ hai.
Khi đó áp suất của hỗn hợp khí trong bình là:
p = p 1 ' + p 2 ' (1)
Xét chất khí trong bình A và B khi khóa K đóng và mở.
Theo định luật Bôi-lơ – Ma-ri-ốt ta có:
p 1 V 1 = p 1 ' ( V 1 + V 2 )
⇒ p 1 ' = p 1 V 1 V 1 + V 2 (2)
p 2 V 2 = p 2 ' ( V 1 + V 2 )
⇒ p 2 ' = p 2 V 2 V 1 + V 2 (3)
Thay (2) và (3) vào (1) ta được:
p = p 1 ' + p 2 ' = p 1 V 1 + p 2 V 2 V 1 + V 2
= 1 , 6.3 + 3 , 4.4 , 5 3 + 4 , 5 = 2 , 68 a t
SS
1 tháng 3 2016
Tính áp suất p' của khí trong bình .
Lúc đầu khí trong bình (1) có \(\begin{cases}V_1\\p=10^5Pa\\T=300K\end{cases}\) bình (2) có: \(\begin{cases}V_2=2V_1\\p\\T\end{cases}\)
Số mol khí trong hai bình \(n=\frac{3pV_1}{RT}\)
Lúc sau, khí trong bình (1) có \(\begin{cases}V_1\\p'\\T_1=273K\end{cases}\) bình (2) có \(\begin{cases}V_2=2V_1\\p'\\T_2=330K\end{cases}\)
Số mol khí trong bình (1): \(n_1=\frac{p'V_1}{RT_1}\), trong bình (2): \(n_2=\frac{2p'V_1}{RT_2}\)
\(n=n_1+n_2\Leftrightarrow\frac{3pV_1}{RT}=\frac{p'V_1}{RT_1}+\frac{2p'V_2}{RT_2}\)
\(\frac{3p}{T}=p'\left(\frac{1}{T_1}+\frac{2}{T_2}\right)\) suy ra \(p'=1,024.10^5Pa\)
