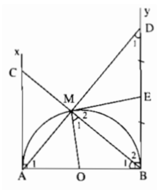
Cho nửa đường tròn tâm O,đường kính BC.Điểm A thuộc nửa đường tròn đó.Vẽ hình vuông ABED thuộc nửa mặt phẳng bờ AB,không chứa đỉnh C.Gọi F là giao điểm của AE và nửa đường tròn tâm O.K là giao điểm của CF và ED
a] CMR bốn điểm E,B,F,K nằm trên một đường tròn
b Tam giác BKC là tam giác gì Vì sao
c Khi điểm A di động trên nửa đường tròn tâm O thì điểm E di chuyển trên đường nào