Tham gia phong trào trồng cây xanh ba lớp 7A , 7B , 7C đã trồng đc tất cả 100 cây xanh. Số cây của lớp 7A trồng đc bằng \(\frac{5}{3}\)số cây của lớp 7B trồng được và số cây của lớp 7C trồng được bằng \(\frac{1}{4}\)tổng số cây của hai lớp 7A, 7B trồng được . Tính số cây của mỗi lớp đã trồng.
P/s : Treo giải ạ : Nhanh nhất + đúng : 6 tick ((=

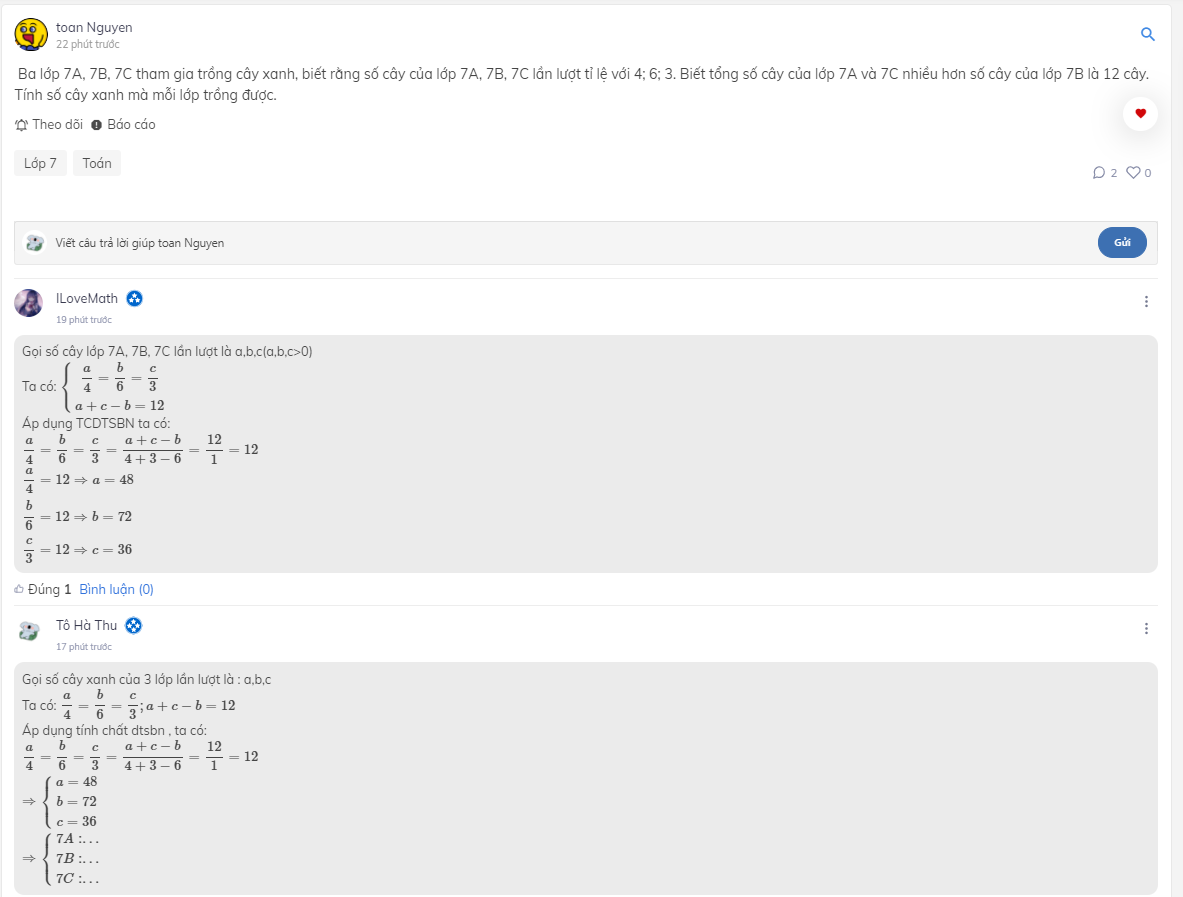
Lớp 7C trồng được số cây là:
100 : (1 + 4) x 1 = 20 (cây)
Lớp 7A và 7B trồng được số cây là:
100 - 20 = 80 (cây)
Lớp 7A trồng được số cây là:
80 : (5 + 3) x 5 = 50 (cây)
Lớp 7B trồng được số cây là:
80 - 50 = 30 (cây)
Đ/S: Lớp 7A: 50 cây
Lớp 7B: 30 cây
Lớp 7C: 20 cây
Chúc bạn học tốt !!!
Em học lớp 5 nên chỉ giải được cách đó thôi anh
Lớp 7C trồng được số cây là:
100 : (1 + 4) x 1 = 20 (cây)
Lớp 7A và 7B trồng được số cây là:
100 - 20 = 80 (cây)
Lớp 7A trồng được số cây là:
80 : (5 + 3) x 5 = 50 (cây)
Lớp 7B trồng được số cây là:
80 - 50 = 30 (cây)
Đ/S: Lớp 7A: 50 cây
Lớp 7B: 30 cây
Lớp 7C: 20 cây
Chúc bạn học tốt !!!
Em học lớp 5 nên chỉ giải được cách đó thôi anh