Gọi M, m lần lượt là giá trị lớn nhất , giá trị nhỏ nhất của hàm số y = x(2017 +\(\sqrt{2019-x^2}\)) trên tập xác định của nó . Tính M-m
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
.
.
.
.
CM
22 tháng 12 2018
Chọn D
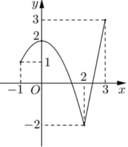
Đặt t = -sinx + 2 vì 
Xét hàm số y = f(t) với 
từ đồ thị đã cho, ta có:
3 tháng 1 2021
Đặt y= f(x) = \(x^2-2\left(m+\dfrac{1}{m}\right)x+m\)
Hoành độ đỉnh của đồ thị hàm số x=\(m+\dfrac{1}{m}\ge2\) (BĐT co-si)
vì hệ số a =1>0 nên hàm số nghịch biến trên \(\left(-\infty;m+\dfrac{1}{m}\right)\)
Suy ra, hàm số nghịch biến trên \(\left[-1;1\right]\)
=> y1 = f(-1) = \(3m+\dfrac{2}{m}+1\)
y2 = f(1)=\(1-m-\dfrac{2}{m}\)
theo đề bài ta có : y1-y2=8 <=> \(3m+\dfrac{2}{m}+1-1+m+\dfrac{2}{m}=8\left(m>0\right)\)
<=> \(m^2-2m+1=0\)
<=> m=1
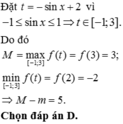
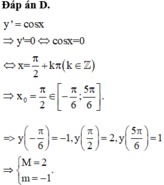
đây là đáp án