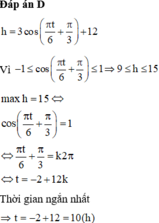Hàng ngày, mực nước của một con kênh lên xuống theo thủy triều. Độ sâu h (mét) của mực nước trong kênh tính theo thời gian t (giờ) trong một ngày 0<t<24)với công thức (\(h=cos\left(\dfrac{\pi t}{6}+1\right)+12\) .Một con tàu cần qua kênh khi độ sâu của nước là 11 mét, hỏi tàu có thể qua trong khoảng thời gian nào trong ngày?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Cách giải:
Đặt π t 14 = u ⇒ u ∈ 0 ; 12 π 7 khi đó ta có h = 2 sin 3 u 1 − 4 sin 2 u + 12
Đặt ⇔ h = 2 3 sin u − 4 sin 3 u 1 − 4 sin 2 u + 12
6 t − 24 t 3 − 8 t 3 + 32 t 5 + 12
32 t 5 − 32 t 3 + 6 t − 12
Xét u ∈ 0 ; π 2 ⇒ v ∈ 0 ; 1
Dùng [MODE] [7] ta có  : trong khoảng có 1 lần hàm số đạt giá trị bằng 13.
: trong khoảng có 1 lần hàm số đạt giá trị bằng 13.
 trong khoảng có 1 lần hàm số đạt giá trị bằng 13.
trong khoảng có 1 lần hàm số đạt giá trị bằng 13.
 trong khoảng có 1 lần hàm số đạt giá trị bằng 13.
trong khoảng có 1 lần hàm số đạt giá trị bằng 13.
Vậy v ∈ 0 ; 1 thì có 3 lần f v = 13.
Xét u ∈ π 2 ; π ⇒ v ∈ 0 ; 1 . Tương tự như trên ta có 3 lần f v = 13.
Xét u ∈ π ; 3 π 2 ⇒ v ∈ − 1 ; 0 có 2 lần f v = 13.
Xét u ∈ 3 π 2 ; 12 π 7 ⇒ v ∈ − 1 ; sin 12 π 7 ⇒ có 1 lần f v = 13.
Vậy có tất cả 9 lần mực nước trong kênh đạt độ sâu 13m.

Đáp án D
h = 1 2 cos π t 8 + π 4 + 3 ≤ 1 2 + 3 = 7 2
Đẳng thức xảy ra khi cos π t 8 + π 4 = 1 ⇔ π t 8 + π 4 = k 2 π ⇔ t = 14 k
Do k ∈ ℤ và 0 h ≤ t ≤ 24 h nên k = 1 . Vậy
t = 14 h

Đáp án D
h = 3 cos π t 6 + π 3 + 12
Vì − 1 ≤ cos π t 6 + π 3 ≤ 1 ⇒ 9 ≤ h ≤ 15
max h = 15 ⇔ cos π t 6 + π 3 = 1 ⇔ π t 6 + π 3 = k 2 π ⇔ t = − 2 + 12 k
Thời gian ngắn nhất ⇒ t = − 2 + 12 = 10 ( h )

\(h=3cos\left(\dfrac{\pi t}{6}+\dfrac{\pi}{3}\right)+12\le3.1+12=15\left(m\right)\)
" = " \(\Leftrightarrow\dfrac{\pi t}{6}+\dfrac{\pi}{3}=2k\pi\left(k\in Z\right)\) \(\Leftrightarrow\dfrac{t}{6}+\dfrac{1}{3}=2k\Leftrightarrow t=12k-2\)
t min ; t > 0 \(\Rightarrow k=1\) thì t = 10 (h)